Sabemos que a Geometria Plana é o assunto mais importante em provas de vestibular, e esse assunto é cobrado desde a 8⁰ ano do ensino fundamental. Todas as figuras planas são muito importante no contexto geral, mas a figura mais estudada é certamente o triângulo. Nesse post iremos estudar a teoria além de resolver exercícios sobre os elementos e pontos notáveis de um triângulo !

O triângulo apresenta muitas estruturas e classificações, vamos começar com os elementos de um triângulo.

Abaixo assista ao vídeo de teoria e uma lista de exercícios sobre elementos e pontos notáveis de um triângulo

Elementos e Pontos Notáveis de um Triângulo

Elementos de um Triângulo

Elementos e Pontos Notáveis de um Triângulo

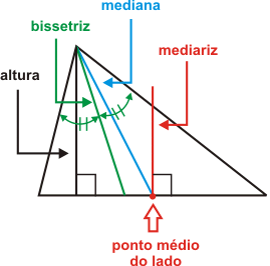
       Elementos de um Triângulo

Altura:

De forma muito simples podemos dizer que a altura é um segmento de reta que uni a base com o vértice oposto formando um ângulo reto com esta.

Bissetriz:

segmento de reta que divide ao meio o ângulo interno desse vértice. Isso significa que esse dois novos ângulos divididos pela reta chamada bissetriz são iguais ou congruentes.

Mediana:

é o segmento de reta que uni o ponto médio da base com o vértice oposto.

Mediatriz:

é mais um segmento de reta que sempre parte de um ponto médio de uma das bases e formando um ângulo reto com a mesma.

Ceviana:

 é qualquer segmento de reta que parte de um vértice de um triângulo e corta o lado oposto a esse vértice.

São 3 as Cevianas de um triângulo, são elas: Bissetriz, Mediana e Altura.

PONTOS NOTÁVEIS DE UM TRIÂNGULO

1) ORTOCENTRO

é o primeiro ponto notável e o ortocentro significa o Ponto de Encontro das 3 Alturas

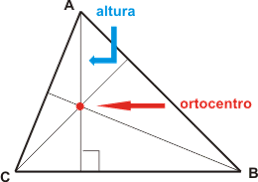
Pontos notáveis de um Triângulo

2) INCENTRO:

Ponto de Encontro das 3 Bissetrizes

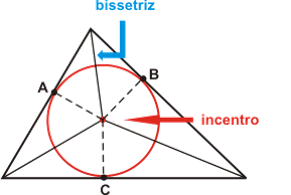
            incentro

Uma dica para encontrar o incentro é só buscar  o centro de uma circunferência que está inscrita no triângulo, la será o incentro 

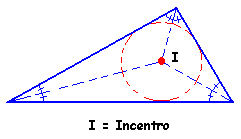
pontos notáveis incentro

3) BARICENTRO:

é o Ponto de Encontro das 3 Medianas.

Uma dica para encontrar  o baricentro é buscar o centro de gravidade do triângulo.

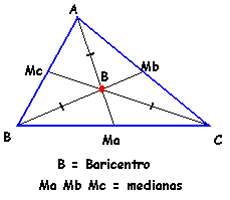
         Baricentro

4) CIRCUNCENTRO:

Ponto de Encontro das 3 Mediatrizes

A dica para encontrar o circuncentro é buscar o centro de uma circunferência circunscrita no triângulo.

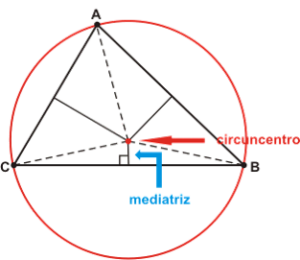
                       Circuncentro

Pontos Notáveis nos triângulo equilátero e Isósceles.

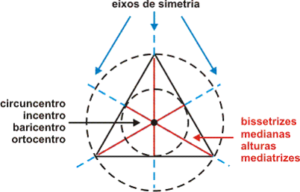
Pontos notáveis do triângulo equilátero

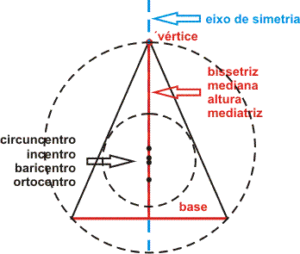
Pontos notáveis do triângulo isósceles

Veja aqui também outras aulas que podem ajudar você:

1.  Congruência e semelhança de figuras planas
2.   Retas e ângulos – Retas
3. Ângulos correspondentes, alternos e colaterais
4. Ângulos da Circunferência 
5. Métodos de Resolução e Discussão de Sistemas de Equações [Vídeo]
6. Produtos Notáveis Como Você Nunca Viu

Exercícios

1) Considerando seus conhecimentos sobre triângulos, cevianas e pontos notáveis, julgue os itens a seguir em V (verdadeiro) ou F (falso).

(   ) O baricentro é o ponto de encontro das bissetrizes internas de um triângulo.

(   ) A mediatriz é um segmento de reta com extremidades no vértice do triângulo e no ponto médio do lado oposto a ele.

(   ) As três medianas de um triângulo encontram-se num ponto chamado baricentro.

(   ) O ortocentro sempre é um ponto interno ao triângulo. Uma mediatriz pode não intersectar nenhum vértice do triângulo.

2) Relacione os pontos notáveis de um triângulo (primeira coluna) à respectiva propriedade (segunda coluna).

I. Baricentro

II. Incentro

III. Circuncentro

IV. Ortocentro

(   ) Centro de massa do triângulo.

(   ) Centro da circunferência que passa pelos vértices do triângulo.

(   ) Ponto de encontro das três alturas do triângulo.

(   ) Centro da circunferência interna ao triângulo e tangente aos seus lados. 

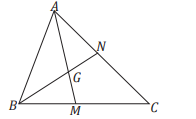
3) No triângulo ABC a seguir, M e N são os pontos médios de BC e de AC, respectivamente. 

Se AM = 12 cm e BN = 15 cm, determine, em cm, o valor de AG + GN.

4) Em um triângulo isósceles ABC, com AB = AC e incentro I, o ângulo interno  mede 100°. Determine a medida do ângulo BÎC.

5) Um triângulo ABC é retângulo em Â. Se =35°, calcule o ângulo formado entre a altura AH e a bissetriz AS desse triângulo.

6) Um triângulo ABC, retângulo em A, é tal que um de seus ângulos internos mede 20°. Determine a medida do ângulo formado entre a altura AH e a mediana AM relativas à hipotenusa BC  desse triângulo , sabendo que AM = MC.

Respostas

1) F   F    V   F   V.

2) I, III, IV, II.

3) 13 cm.

4) 140°.

5) 10°.

6) 50°