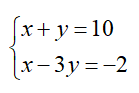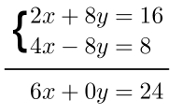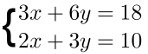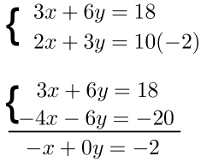Muitos problemas do nosso cotidiano podem ser resolvidos partindo de uma montagem de duas equações do primeiro grau, contendo duas incógnitas.  Veja aqui nesse artigo, os principais métodos de resolução e discussão de Sistemas de Equações de 1° Grau.

E para facilitar a sua compreensão, assista ao vídeo com resoluções de 6 problemas e mais as técnicas de discussão de sistemas. 

Para melhorar o seu entendimento veja alguns problemas resolvidos de sistema nos vídeos abaixo. Esses vídeos tornarão esse estudo muito simples de entender. 

Métodos de Resolução e Discussão de Sistemas de Equações

Assim sendo, essas equações serão calculadas através de um sistema de equações do 1º grau contendo duas variáveis. Essas equações são estruturadas por uma chave que as conterá .

Exemplo: 

Os valores correspondentes ao par ordenado ( x , y)  que verifica a igualdade das duas equações  é a solução do sistema em questão.

Veja que no sistema acima o par ordenado (x , y) corresponde a (7,3)!

Veja que ao substituirmos o 7 no lugar de x e 3 no de y, teremos a verificação da igualdade!

7 + 3= 10    e  7 – 3.3 = -2

Vamos resolver sistemas usando os dois métodos mais simples. São eles o método de adição e o método de substituição

Métodos de Resolução e Discussão de Sistemas

Método da substituição

Vamos entender o método da substituição usando alguns passos bem simples:

   Resolva:

1º passo: Isolar uma das incógnitas em qualquer uma das equações. Nesse caso isolaremos o x da segunda equação!

x -3y = -2

x = 3y – 2

2º passo: Substituir o valor de x, que foi isolado na segunda equação, na primeira equação! Dessa forma obteremos uma equação do 1° grau com apenas uma variável!

Substituir  x = 3y – 2 na primeira equação: x+ y = 10,

logo: 3y – 2 + y = 10 

3º passo: Resolver a equação que possui apenas a variável y do passo 2:

3y – 2 + y = 10 

4y = 10 + 2

y = 12/4

y = 3

4º passo: agora é só substituir o valor de y = 3, encontrado no passo anterior, em qualquer uma das duas equações do nosso sistema:

Vamos substituir na equação dois:   x – 3y = -2

Como y = 3 teremos:

x – 3.3 = -2

logo x = -2 + 9

 x = 7

Então o conjunto solução do sistema é S = {3 , 7}

Métodos de Resolução e Discussão de Sistemas

Método da Adição

1º Tipo: Equações com opostos aditivos

1º passo: Verificar se as duas equações apresentam incógnitas com opostos aditivos

No sistema abaixo, veja que somando-se as equações, eliminamos a incógnita y, pois as duas equações apresentam opostos aditivos nos termos com a varável y.

8y e -8y são chamados de opostos aditivos

Somando os termos do lado esquerdo temos e igualando a soma do lado direito teremos:

2x + 4x + 8y + (– 8y) = 16 + 8

Agora é só isolar a variável que ficou, nesse caso x!

6x = 24

x = 24/6

x = 4

2º passo:

Substituir o valor numérico encontrado em qualquer uma das equações do nosso sistema.

Substituiremos o valor de x = 4 na segunda equação: 4x – 8y = 8

4 .4 – 8.y = 8

16 – 8 = 8y

8y = 8

y = 1

Logo a solução do sistema é S = {4, 1}.

2º Tipo: Equações sem opostos aditivos

Ou seja, quando a soma dos termos não zera uma das incógnitas

Observe que no sistema acima  os coeficientes da incógnita x e da incógnita y não são opostas aditivas. Pois se somarmos as duas equações nenhuma variável será eliminada!

Nesse caso será preciso usar um artifício e criar a oposta aditiva pela multiplicação de um número específico, baseado nos valores que o sistema nos fornece. E só depois desse passo deveremos somar as equações 

Veja aqui se somarmos teremos: 

     5x + 9y = 28

Então para eliminar uma das incógnita, precisaremos multiplicar a segunda equação por -2, por exemplo!

Note que, devemos multiplicar todos os termos da segunda equação por -2, e só depois disso deveremos somar as equações para eliminar a incógnita y!

– x = – 2

  x = 2

Agora é só substituir o valor encontrado em qualquer uma das equações do nosso sistema!

Vamos substituir o valor x = 2 na segunda equação, para exemplificar:

2x + 3y = 10

2.2 + 3.y = 10

3y = 10 -4

y = 6/3

y = 2

Logo o conjunto solução é S = {2, 2}

DISCUSSÃO DE SISTEMAS

Métodos de Resolução e Discussão de Sistemas

Agora vamos entender como esses sistemas poderão ser chamados:

Em todo sistema de duas equações do 1° grau temos a seguinte estrutura:

Para poder classificar o sistema devemos observar apenas as relações entre os coeficientes das variáveis que o mesmo apresenta:

I) Sistema possível e determinado – (SPD)

Apresenta uma única solução!

Graficamente as retas serão concorrentes, ou seja com apenas um ponto em comum

^{Retas Concorrentes}

Métodos de Resolução e Discussão de Sistemas

II) Sistema possível e indeterminado (SPI)

Teremos aqui infinitas soluções ou seja infinitos pontos em comum

As retas das equações do nosso sistema serão coincidentes

^{Retas Coincidentes}

III) Sistema impossível (SI)

O sistema não  apresentará solução

Sistema sem solução

As retas das equações do nosso sistema serão paralelas

^Paralelas

Métodos de Resolução e Discussão de Sistemas

Pratique!

1) Classificar ou discutir os sistemas abaixo

A) 

Resposta:

Comparando as relações entre os coeficientes das equações, teremos:

B) Classificar ou discutir os sistemas abaixo

Resposta:

Comparando as relações entre os coeficientes das equações, teremos:

Logo, o sistema é possível indeterminado.