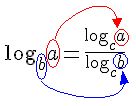Mudança de Base a Questão Difícil de Logaritmo [Vídeo]

    Logaritmo é um conteúdo normalmente visto no primeiro ano do segundo grau. Ele é dividido em muitos tópicos importantes. São eles: Definição, Consequência da definição, propriedades, equações e  inequações logarítmicas, gráficos e mudança de base.

        Para principiantes ou neófitos da Matemática, identificar a operação de mudança de base é muito difícil. Mas agora vamos mostrar de forma fácil essa situação.

Antes  vamos entender alguns princípios e conceitos básicos de Mudança de Base:

Matemática para Enem e vestibular

Temos inicialmente o logaritmo de “a” na base “b”:    log_ba

Após a aplicação da Mudança de base teremos o aparecimento da base “c”.

O logaritmando “a” e a base  “b” recebem um logaritmo independente e transformam-se em um quociente de logaritmos, com bases que podem ser escolhidas conforme a necessidade.

Veja:

Mudança de base

Quando usar:

Situação 1 para mudança de Base:

Quando tivermos nos dados do problema logaritmos com bases diferentes do que está sendo pedido.

Exemplo:

Dados log 2 = 0,301 e  log 3 = 0,477. Calcule o valor do  log23

Veja que nos dados do problema temos dois logaritmos de base 10 e é pedido o valor do  log23 (com base 2)

Resolução:

 log23 = log 3 / log 2 = 0,477 / 0,301 =

Resposta = 2,558

Veja ao vídeo que explica essa operação de mudança de base:

Situação 2 para mudança de Base:

Quando tivermos numa equação logarítmica, uma soma de logaritmos de bases diferentes

Exemplo:

Se log₂x + log₈x = 4, então o valor de x é :

Resoluçao:

log₂x + log₂x / log₂8 = 4

log₂x + log₂x / 3 = 4

(3.log₂x + log₂x) / 3 = 4

3.log₂x + log₂x = 4.3

4.log₂x = 12

log₂x = 12/4

log₂x = 3

x = 2³

Resposta = 8

Situação 3 para mudança de Base:

Quando tivermos uma multiplicação de logaritmos com bases diferentes

Exemplo:

Calcule o valor de:

log₃7 . log₇9 = 

Aplicando a mudança de base em ambos logaritmos temos: 

(log7 / log3) . (log9 / log7)  =

Simplificando o log7 em cima e em baixo ficamos com:

log9 / log3 =

Nesse momento podemos usar a operação de mudança de base ao contrário, fazendo o logaritmando do log de 3 se tornar uma base:

log₃9 =

Resolvendo teremos:

log₃9 = x

3 ^x = 9

3 ^x = 3²

Resposta: x = 2