Grandezas Proporcionais – O que mais cai no Enem
Descubra o que são as grandezas diretamente e inversamente proporcionais e se dê bem nas provas do ENEM
Entenda o que são as grandezas proporcionais e se dê bem na Matemática do Enem, já que esse conteúdo cai muito nessa prova!!
Grandezas é tudo aquilo que pode ser medido ou mensurado. Como exemplos de grandezas poderíamos citar: velocidade, distância, tempo, altura, potência…
Duas grandezas, quando comparadas podem ser diretamente proporcionais ou inversamente proporcionais.
O que são grandezas diretamente proporcionais?
Podemos dizer que duas grandezas são diretamente proporcionais quando ambas aumentam ou diminuem ao mesmo tempo.
Exemplo:
Tempo e distância são grandezas diretamente proporcionais!
Quanto mais tempo ficamos dirigindo em uma estrada, maior distância percorreremos.
Observe que a velocidade pode ser representado por uma razão (divisão) e é calculada por:
Velocidade = Distância/tempo
Há uma proporção que pode ser representado por uma relação de igualdade entre duas ou mais razões (divisões) dessa forma podemos comparar duas grandezas em diferentes situações.
a/b = c/d
Essa relação pode ser entendida da seguinte maneira: a está para b, assim como c está para d.
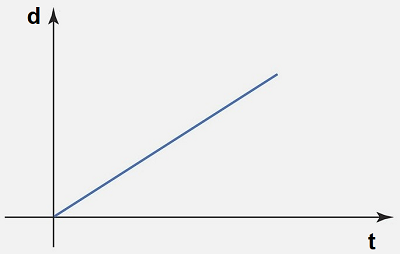
Podemos representar graficamente a variação de duas grandezas diretamente proporcionais (distância e velocidade) através de uma reta, Partindo da fórmula da física
v = d/t, sendo v a velocidade uma constante.
Exemplo de proporcionalidade direta
Agora, veremos com números a relação entre as duas grandezas.
Em uma viagem um ciclista percorre um trajeto com velocidade constante de 20 km/h. Veja na tabela abaixo
| Tempo (h) | 1 | 2 | 3 | 4 |
| Distância (km) | 20 | 40 | 60 | 80 |
A constante de proporcionalidade entre as grandezas é encontrada pela razão entre o tempo de trabalho da máquina e o número de cópias realizadas.
20/1 = 40/2 = 60/3 = 80/4
A razão dessa sequência (20/1), que nesse caso é a velocidade, recebe o nome de constante de proporcionalidade (k) em outras relações de proporcionalidade direta.
Proporcionalidade inversa
Duas grandezas são inversamente proporcionais quando comparadas e relacionadas entre si e uma aumenta e a outra diminui.
Como exemplo podemos citar as grandezas velocidade e tempo
Digamos que um automóvel vai precisar percorrer 400 km em uma viagem Podemos dizer que quanto maior for a velocidade de um automóvel menos tempo ele levará na viagem.
Logo a velocidade e o tempo são grandezas inversamente proporcionais
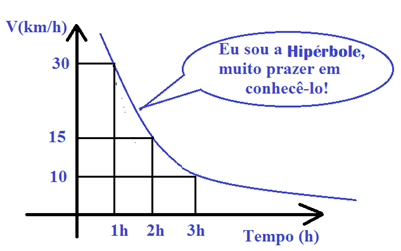
Graficamente a variação inversamente proporcional de uma grandeza em relação à outra forma uma hipérbole, pois temos y = k/x, sendo k uma constante.
Exemplo de proporção inversa
Quando se aumenta a velocidade, o tempo para concluir um percurso é menor. Da mesma forma, ao diminuir a velocidade mais tempo será necessário para fazer o mesmo trajeto.
vamos entender como podemos aplicar a relação entre grandezas inversamente proporcionais.
Pedro resolveu pegar sua bicicleta e medir o tempo que levava da escola para sua casa, ele percorreu esse trajeto com diferentes velocidades.
Veja a tabela
| Tempo (h) | 1 | 2 | 3 | 4 |
| Velocidade (km/h) | 30 | 15 | 10 | 7,5 |
Podemos fazer a seguinte relação com os números das sequências:
1.30 = 2.15 = 3. 10 = 4.7,5 = 30
Reescrevendo como igualdade de razões inversas, temos:
1/(1/30) = 2/(1/15) = 3/(1/10) = 4/(1/7,5)
Nesse exemplo, a sequência de tempo (1, 2, 3, 4) é inversamente proporcional à velocidade média pedalando (30, 15, 10 e 7,5) e a constante de proporcionalidade (k) entre essas grandezas é 30.
Observe que quando um número de uma sequência dobra, o número da sequência correspondente reduz pela metade.
CURSO ONLINE GÊNIO DA MATEMÁTICA
Questões de Grandezas Proporcionais
- Classifique as grandezas relacionadas a seguir em diretamente ou inversamente proporcional.
A) Número de operários e tempo de conclusão de uma obra
B) Velocidade e distância percorrida
C) Velocidade e tempo para concluir um trajeto
D) Consumo de combustível e quilômetros percorridos por um veículo.
E) Quantidade de tijolos e área de uma parede.
F) Desconto dado em um produto e o valor final pago.
G) Número de torneiras de mesma vazão e tempo para encher uma piscina.
2) Um prêmio de R$ 600.000,00 vai ser dividido entre os acertadores de um bingo. Observe a tabela e responda:
a) Qual a razão entre o número de acertadores do prêmio de R$200.000,00 para o prêmio de R$150.000,00?
b) Qual a razão entre os prêmios de 3 e 4 acertadores da tabela acima
c) O número de acertadores e os prêmios são grandezas diretamente ou inversamente proporcionais?AULA 01
Funções 1º Grau [Parte 1]
https://geniodamatematica.com.br/assunto-mais-cobrado-no-enem/
AULA 02
https://geniodamatematica.com.br/o-que-mais-cai-no-enem-em-matematica/
AULA 03
3) Os números x, y e 32 são diretamente proporcionais aos números 40, 72, 128. Determine os números x e y.
4) Enem Nos shopping centers, costumam existir parques com vários brinquedos e jogos. Os usuários colocam créditos em um cartão, que são descontados por cada período de tempo de uso dos jogos.
Dependendo da pontuação da criança no jogo, ela recebe um certo número de tíquetes para trocar por produtos nas lojas dos parques.
Suponha que o período de uso de um brinquedo em certo shopping custa R$ 3,00 e que uma bicicleta custa 9 200 tíquetes.
Para uma criança que recebe 20 tíquetes por período de tempo que joga, o valor, em reais, gasto com créditos para obter a quantidade de tíquetes para trocar pela bicicleta é
a) 153O. b) 460. c) 1218. d) 1380. e) 3066.
5) (ENEM) Em 20 de fevereiro de 2011, ocorreu a grande erupção do vulcão Bulusan nas Filipinas. A sua localização geográfica no globo terrestre é dada pelo GPS (sigla em inglês para Sistema de Posicionamento Global) com longitude de 124° 3’ 0” a leste do Meridiano de Greenwich.
Dado: 1° equivale a 60’ e 1’ equivale a 60”.
A representação angular da localização do vulcão com relação a sua longitude da forma decimal é
a) 124,02°. b) 124,05°. c) 124,20°. d) 124,30°. e) 124,50°.
6) Em um mapa de uma pequena cidade, destaca-se a presença de uma rodovia, cuja extensão é de 15 quilômetros. No mapa em questão, sua medida está em 10 centímetros, o que nos permite concluir que a sua escala cartográfica é de:
a) 1:15.000 b) 1:150.000 c) 1:1.500 d) 1:15 e) 1:100.000
7) Pedro tem uma piscina em sua casa que mede 6 m de comprimento e comporta 30 000 litros de água. Seu irmão Antônio decide também construir uma piscina com a mesma largura e profundidade, mas com 8 m de comprimento. Quantos litros de água cabem na piscina de Antônio?
a) 10 000 L b) 20 000 L c) 30 000 L d) 40 000 L
8) Qual é a velocidade de um automóvel que gasta duas horas em um percurso, sabendo que gastaria 6 horas nesse mesmo percurso se estivesse a 30 km/h?
a) 90 km/h b) 60 km/h c) 30 km/h d) 20 km/h e) 10 km/h
9) (PUC-MG) Certa máquina de calcular faz 200 operações por mi- nuto, enquanto um calculista faz 46 dessas operações no mesmo tempo. Pode-se afirmar que a calculadora é m vezes mais rápida que o calculista. O valor de m é tal que:
a) 1 < m ≤ 4 b) 4 < m ≤ 7 c) 7 < m ≤ 10 d) 10 < m ≤ 13
10) (ENEM) Uma escola lançou uma campanha para seus alunos arrecadarem, durante 30 dias, alimentos não perecíveis para doar a uma comunidade carente da região. Vinte alunos aceitaram a tarefa e nos primeiros 10 dias trabalharam 3 horas diárias, arrecadando 12 kg de alimentos por dia. Animados com os resultados, 30 novos alunos somaram-se ao grupo, e passaram a trabalhar 4 horas por dia nos dias seguintes até o término da campanha. Admitindo-se que o ritmo de coleta tenha se mantido constante, a quantidade de alimentos arrecadados ao final do prazo estipulado seria de:
a)920kg b)800kg c)720kg d)600kg e)570kg
DP = diretamente proporcional
IP, DP, IP, DP, IP e IP
