Como Resolver Potências
Como Resolver Potências
Potenciação – Nesse módulo vamos aprender como resolver potências com exercícios e teoria com gabarito sobre potenciação. Vamos aprender as propriedades, conceitos com testes resolvidos e muito mais. Mostrarei alguns casos com uma explicação detalhada sobre potenciação!
Vamos lá…
Sendo a um número real e n um número natural positivo, temos:
Definição
Como Resolver Potências
Potenciação
Propriedades
Como Resolver Potências
Como Resolver Potências
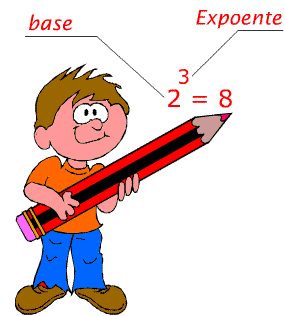
Ao escrever 4x4x4, devemos indicar por por 4³
outro exemplo , 6³ = 6x6x6 = 216
onde : 6 é a base (fator que se multiplica várias vezes)
e 3 é o expoente ( o número de vezes que repetimos a base)
216 é 0 valor encontrado na potenciação (resultado final)
Mais exemplos:
a) 5²= 5×5 = 25
b) 2³= 2x2x2 =8
DICAS
Quando expoente é 2 chamamos de quadrado
Quando expoente é 3 chamamos de cubo
Quando expoente é 5 chamamos quinta potência
Quando expoente é 7 chamamos sétima potência
Também:
a) 9² lemos nove elevado ao quadrado
b) 10³ lemos dez elevado ao cubo
Por convenção temos que:
1) todo o número elevado ao expoente zero o resultado é sempre um
a) 10º=1
b) (-2)º=1
c) (1/7)º=1
2) todo o número elevado ao expoente 1 é igual à própria base,
exemplo
a) (-18)¹ = -18
b) (1/5)¹ = 1/5
c) 5¹ = 5
Como Resolver Potências
EXERCÍCIOS
Em 7² = 49, responda:
a) Qual é a base?
b) Qual é o expoente?
c) Qual é a potência?
Resolva:
a) 0x0x0x0x0=
b) 9x9x9=
c) 2x2x2x2=
d) 4x4x4x4x4
e) 5x5x5x5x5=
f) axaxaxa=
Exercícios resolvidos
a) 3³ = 27
b) 10⁵ =100000
c) 10³ =1000
d) 13² =169
e) 12² =144
f) 20² = 400
Como Resolver Potências
EXERCÍCIOS
1) Descubra o número que :
ao elevarmos ao quadrado dá 49
ao elevarmos ao quadrado dá 100
ao elevarmos ao quadrado dá 225
Respostas: 7,10 e 15
2) Qual o valor de x ?
- x²= 121
- x²= 64
- x²= 225
- x²= 49
Respostas
±11, ±8, ±15 e ±7
Revisão: Regras – Como Resolver Potências
Como Resolver Potências
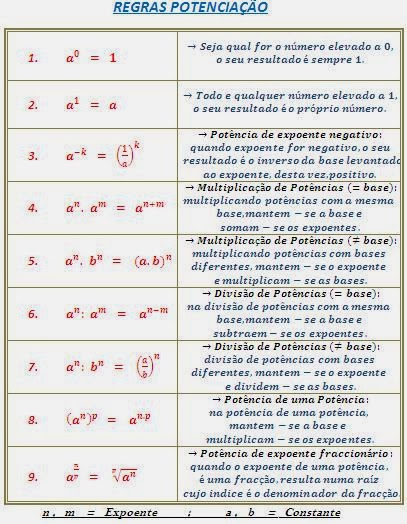
PROPRIEDADES DA POTENCIAÇÃO
Primeira propriedade da potenciação
Multiplicação de potências de mesma base
Ao multiplicar potências de mesma base, repetimos a base e somamos os expoentes.
exemplos
3² x 3⁵ = 3²⁺⁵ = 3⁷
Na multiplicação, potencias de mesma base, conservamos a base e somamos os expoentes.
EXERCÍCIOS RESOLVIDOS SOBRE POTENCIAÇÃO
1) Reduza a uma só potência
a) 4³ x 4 ²= 4⁵
b) 7⁴ x 7⁵ = 7⁹
c) 2⁶ x 2²= 2⁸
d) 6³ x 6 = 6⁴
e) 3⁷ x 3² = 3⁹
f) 9³ x 9 = 9⁴
g) 5 x 5² = 5³
h) 7 x 7⁴ = 7⁵
i) 6 x 6 = 6²
j) 3 x 3 = 3²
l) 9² x 9⁴x 9 = 9⁷
m) 4 x 4² x 4 = 4⁴
n) 4 x 4 x 4= 4³
0) m⁰ x m x m³ = m⁴
p) 15 x 15³ x 15⁴x 15 = 15⁹
2) Reduza a uma só potência:
a) 7² x 7⁶ = 7⁸
b) 2² x 2⁴= 2⁶
c) 5 x 5³ = 5⁴
d) 8² x 8 = 8³
e) 3⁰ x 3⁰ = 3⁰
f) 4³ x 4 x 4² = 4⁶
g) a² x a² x a² = a⁶
h) m x m x m² = m⁴
i) x⁸ . x . x = x¹⁰
j) m . m . m = m³
Segunda Propriedade da potenciação
Divisão de Potência de mesma base
Ao dividir potências de mesma base, repetimos a base e subtraímos os expoentes.
Exemplo
a) 8⁹: 8² = 8⁹⁻² = 8⁷
b) 5⁴ : 5 = 5⁴⁻¹ = 5³
Então, na divisão, potencias de mesma base, conservamos a base e subtraímos os expoentes!
EXERCÍCIOS DE POTENCIAÇÃO
1) Reduza essa sequencia de divisão a uma só potência
a) 5⁴ : 5² = 5²
b) 8⁷ : 8³ = 8⁴
c) 9⁵ : 9² = 9³
d) 4³ : 4² = 4¹
e) 9⁶ : 9³ = 9³
f) 9⁵ : 9 = 9⁴
g) 5⁴ : 5³ = 5¹
h) 6⁶ : 6 = 6⁷
i) a⁵ : a³ = a²
j) m² : m = m¹
k) x⁸ : x = x⁷
l) a⁷ : a⁶ = a¹
m) 13⁵ : 13³ =
n) 42⁸ : 42³=
o) 27⁴ : 27 =
p) 135⁹ : 135³ =
q) 831⁴ : 831⁰ =
r) 43⁰ : 43⁰ =
Terceira Propriedade da potenciação
Potência de Potência
Ao elevar uma potência a um outro expoente, repetimos a base e multiplicamos os expoentes.
(9²)³ = 9⁶ lembrando que quando tem parênteses multiplicamos os expoentes 2×3
conclusão: conservamos a base e multiplicamos os expoentes.
Veja também como Resolver equações do primeiro grau: COMO RESOLVER EQUAÇÕES DO PRIMEIRO GRAU
EXERCÍCIOS
1) Resolva:
a) (4⁴)²
b) (3²)⁴
c) (6²)⁵
d) (8³)²
e) (0⁴)⁴
f) (6²)⁷
g) (9³)⁵
h) (x²)³
i) (a³)⁴
j) (d³)⁴
k) (v⁵)²
l) (y³)⁰
m) (m⁵)⁰
2) Reduza a uma só potência:
a) (7²)³ =
b) (4⁴)⁵ =
c) (8³)⁵ =
d) (2⁷)³ =
e) (a²)³ =
f) (m³)⁴ =
g) (a⁴)⁴ =
h) (m²)⁷ =
Curso Online de Matemática
