Como Resolver Equações Fracionárias

Esse tipo de equação é muito frequente  e está presente em boa parte das provas de Matemática. Antes de entender como resolver equações fracionárias , vamos aprender a sua definição e conhecer a propriedade fundamental da proporção.

Veja aqui Como Resolver Equações do Primeiro Grau

Veja aqui Como Resolver Equações do segundo Grau

Saiba tudo sobre o Enem Aqui: http://geniodoenem.com.br/

DEFINIÇÃO

Chama-se equações fracionárias numa incógnita todas as equações cuja variável figura no denominador.

Abaixo segue um exemplo de equação fracionária:

2(x + 2) + 5 =   57
       x                     3

Nesta equação fracionária, observamos que:

• O primeiro membro é       2(x + 2) + 5
                                             x
• O segundo membro é        57/3

 Propriedade fundamental da proporção

Veja a fração 5/8 ; se multiplicarmos por 2 o denominador e o numerador, não estaremos alterando o valor da fração e ela ficará 10/16.

Podemos então dizer que:

5 = 10 ou 5 : 8 = 10 : 16
8    16

Os números 5, 8, 10 e 16 são os termos dessa proporção sendo que 5 e 16 são os termos dos extremos e 8 e 10 são os termos dos meios.

Propriedade: O produto dos meios é igual ao produto dos extremos

Produto dos termos dos meios: 8 x 10 = 80
Produto dos termos dos extremos: 5 x 16 = 80

usada nas resoluções de equações Fracionárias

Como Resolver Equações Fracionárias

Verificamos assim que ela é verdadeira e será muito acionárias

Resolução Exemplo 1: 

2 = x – 1
x     x + 2

Como os denominadores precisam ser diferentes de zero, teremos:  x ≠ 0 e x ≠ -2

Para resolver essa equação fracionária devemos aplicar a propriedade das proporções:

2(x + 2) = x(x – 1)

Como Resolver Equações Fracionárias

Agora precisamos aplicando a propriedade distributiva:

EQUAÇÕES FRACIONÁRIAS – PROPRIEDADE DISTRIBUTIVA

2x + 4 = x² – x

Passando dos os termos para o lado esquerdo da equação teremos:

0 = x² – x  – 2x – 4

Somando os termos semelhantes chegamos em uma equação do segundo grau.

x² – 3x – 4 = 0

Aplicando a fórmula de Bháskara:

a = 1,   b = – 3    e       c = – 4.

x = –b ± √(b² – 4ac)
2a

x = –(–3) ± √((–3)² – 4.1.(–4))
2.1

x = +3 ± √(9 + 16)
2

x = 3 ± √25
     2

x = 3 ± 5
     2

x’ = 3 + 5 = 8 = 4
     2        2

x” = 3 – 5 = – 2 = –1
2           2

Chegamos finalmente ao resultado das raízes: x = 4 e x = – 1.

Como Resolver Equações Fracionárias

Resolução – Exemplo 2:

3 = 5 + 1
2     x    5

Nessa equação temos x no denominador e esse nunca poderá ser igual a zero logo: x ≠ 0.

Vamos começar tirando  mínimo múltiplo comum dos denominadores 2, 5 , que é 10. Logo após faremos a soma das frações do lado esquerdo.

3  = 10.5 + 2x.1
2           10x

3  = 50 + 2x
2       10x

Agora vamos aplicar:

3.10x = 2(50 + 2x)

Resolvendo a equação, temos:

30x = 100 + 4x
30x – 4x = 100
26x = 100

  x = 100     
  26

Que simplificando fica:
x = 50
       13

^{Logo a raiz  da  equação é 50}/₁₃

                        Faça a Diferença, Seja um Gênio Você Também!

Como Resolver Equações Fracionárias

Resolução – Exemplo 3:

   2    +    1    +     2    =     1    
x        x–2        x+2       x²–4

Nessa equação temos x, x-2, x+2 e x²–4  nunca poderão ser igual a zero por fazerem parte dos denominadores dos termos da equação logo:

x ≠ 0
x–2 ≠ 0 → x ≠ 2
x+2 ≠ 0 → x ≠ 2
x² – 4 ≠ 0 → x² ≠ 4 → x ≠± √4 → x ≠ ±2

Como Resolver Equações Fracionárias

Para resolver essa equação fracionária precisamos do conhecimento de um dos produtos notáveis:

O produto da soma pela diferença de dois termos

Se tivermos o produto da soma pela diferença de dois termos, poderemos transformá-lo numa diferença de quadrados.

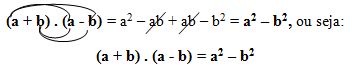
O produto da soma pela diferença de dois termos é igual ao quadrado do primeiro termo, menos o quadrado do segundo termo.

Nesse caso temos: x²–4 = (x+2)(x–2)

   2    +    1    +     2    =          1          
x        x–2      x+2      (x+2)(x–2)

Tirando o mínimo múltiplo comum entre x , x–2 e x+2 no lado direito da equação fracionária teremos:

2.(x+2).(x–2) + 1x.(x+2) + 2x.(x–2) =          1          
                      x(x+2)(x–2)                               (x+2)(x–2)

Podemos agora verificar que ao aplicar a propriedade “produto dos meios = produto dos extremos”, poderemos simplificar os denominadores!

2.(x+2).(x–2) + 1x.(x+2) + 2x.(x–2) =          1          
                  x(x+2)(x–2)                                 (x+2)(x–2)

Passando o x multiplicando o número 1 (lado direito):

2.(x+2).(x–2) + 1x.(x+2) + 2x.(x–2) = 1.x

Aplicando a propriedade distributiva e somando:

2(x²–4) +1x.(x+2) + 2x.(x–2) – x = 0

2x² – 8 + x² + 2x + 2x² – 4x – x = 0

5x² – 3x – 8 = 0

Aplicando a fórmula de Bháskara:

a = 5,   b = – 3    e    c = – 8.

x = –b ± √(b² – 4ac)
2a

x = –(–3) ± √((–3)² – 4.5.(–8))
2.5

x = 3 ± √(9 + 160)
10

x’= 3 ± √169
10

x = 3 ± 13
      10

x’ = 3 +13
      10

x’ = 16
         10

x’ =8/5

x” = 3 – 13
         10

x” = – 10
        10

x” = – 1

Chegamos finalmente ao resultado das raízes: 8/5  e – 1