Como Resolver Equação do 2º grau por Bháskara ou Soma e produto
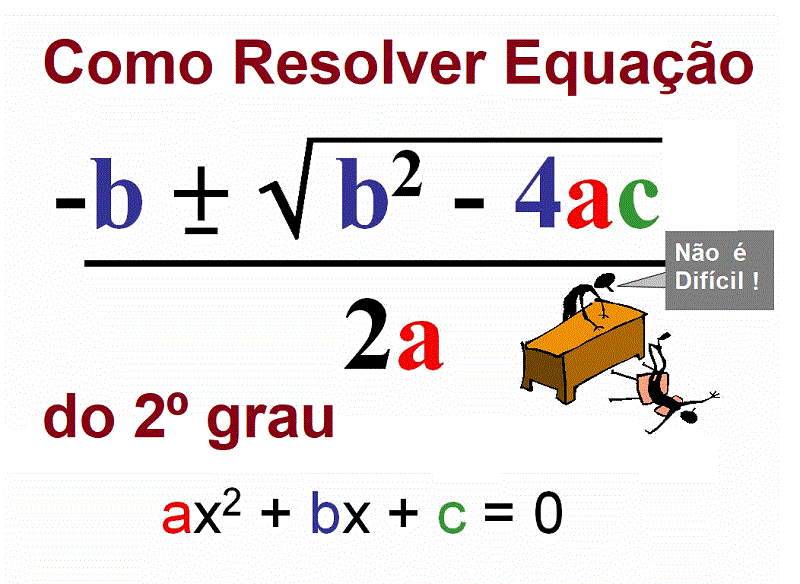
São muitas formas de se resolver uma equação do segundo grau, mas a mais conhecida é a resolução pelo método de Bháskara. Mostraremos também como resolver equação do 2º grau usando o método da soma e do produto das raízes.
Toda equação é uma igualdade, e o número correspondente ao grau é o expoente máximo da variável X. Nesse caso estamos falando de uma equação do segundo grau, logo teremos aqui a variável ou incógnita sempre com expoente máximo igual a 2.
Veja aqui Como resolver equação Fracionárias
Veja aqui Como Resolver Equações do Primeiro Grau
Saiba tudo sobre o Enem Aqui: http://geniodoenem.com.br/
Como Resolver Equação do 2º grau
Como reconhecer o grau de uma equação
- Na matemática, uma equação é uma igualdade envolvendo uma ou mais incógnitas (valores desconhecidos)
Nesses exemplo: x² – 10.x + 24 = 0 a letra x é a incógnita da equação e ela será o número que deverá ser substituído por x para que a função dada fique igual a zero.
A função y = x² – 10.x + 24 é uma expressão matemática que possui duas incógnitas, coeficientes, expoentes e um sinal de igualdade. Ao substituir um valor real qualquer pela variável independente x, acharemos o valor da variável dependente y, ou seja o valor da f(x).
Porém na equação do segundo grau, acharemos apenas os “zeros da função”, ou seja os números que serão substituídos em x para que o valor da função “y” fique igual a zero.
O grau depende do valor de maior expoente. Veja nos exemplos abaixo:
- 5x + 10 = 0. O maior expoente da variável x é um. Então, essa equação é de grau 1 ou de 1º grau.
- 3x² – 5x + 8 = 0. Veja que aparece nesse exemplo duas variáveis x, uma de grau 1 e a outra de grau 2. Vale então o maior expoente para classificarmos a equação que nesse caso é de 2º grau.
- x³ – 3x² + 5x – 9 = 0. Da mesma forma temos aqui uma equação de grau 3 ou seja do terceiro grau (3º grau).
O que são os zeros da função ou raízes da equação do 2º grau?
Ao resolvermos a equação do 2º grau x² – 10x + 24 = 0 pelos 2 métodos que mostraremos a seguir acharemos que 4 e 6 são raizes dessa equação. Isso significa que ao substituirmos qualquer um desses dois valores na função, teremos a soma de toda expressão igual a zero. Veja abaixo:
Substituindo x = 4 na função, temos:
x² – 10.x + 24 = 0
4² – 10.4 + 24 = 0
16 – 40 + 24 = 0
–24 + 24 = 0
0 = 0
Substituindo x = 6 na equação, temos:
x² – 10.x + 24 = 0
6² – 10.6 + 24 = 0
36 – 60 + 24 = 0
– 24 + 24 = 0
0 = 0
E é por isso que o grau é dois, pois temos dois valores que zeram essa função, ou seja temos duas raízes.
Veja abaixo como Resolver Equação do 2º grau Completa
Método de Bháskara
Veja abaixo como resolver equação do 2º grau Incompleta
Resolver Equação do 2º grau Completa
Método de Bháskara
Toda equação do 2º grau tem a seguinte estrutura:
ax² + bx + c = 0, onde a, b e c são os coeficientes.
O valor de “a” sempre estará multiplicando a variável contendo x elevado a dois.
O valor de “b” sempre estará multiplicando a variável contendo x elevado a um
O valor de “c” sempre estará multiplicando a variável contendo x elevadona zero ou seja será o termo independente de x
Como Resolver Equação do 2º grau
Logo, os coeficientes da equação x² + 2x – 15 = 0 são a = 1, b = 2 e c = -15.
Vamos resolver a equação x² + 2x – 15= 0 pelo método de Bháskara!
Aqui está a fórmula que facilita a resolução:
FÓRMULA DE BHÁSKARA
x² + 2x – 15 = 0 são a = 1, b = 2 e c = -15.
1º passo: Encontrar o valor do delta (∆)
∆ = b² – 4 . a . c
∆ = (2)² – 4 . 1 . (–15)
∆ = 4 + 60
∆ = 64
2º passo: Achar as duas raízes
x = – b ± √∆
2∙a
x = – 2 ± √64
2∙1
x = -2 ± 8
2
x’ = –2 + 8 = 6 = 3
2 2
x” = -2 – 8 = – 10 = – 5
2 2
Os resultados são x’ = 3 e x” = –5.
Como Resolver Equação do 2º grau
Exemplo II: Determinar a solução da seguinte equação do 2º grau: x² – 9x = 0.
Os coeficientes são: a = 1, b = 9 e c = 0
Temos aqui um caso de equação do segundo grau incompleta, onde o termo independente “c” é nulo.
∆ = b² – 4 . a . c
∆ = 9² – 4 . 1 . 0
∆ = 81 – 0
∆ = 0
x = – b ± √∆
2∙a
x = – 9 ± √81
2∙1
x’ = –9 + 9 = 0
2
x” = –9 – 9 = – 9
2
Como Resolver Equação do 2º grau com Delta negativo (∆<0)
Quando o delta dá um valor negativo, teremos sempre duas raízes complexas. Esse estudo dos “Números Complexos” normalmente é feito no último ano do segundo grau.
Para resolver esse tipo de equação precisamos saber apenas que ‘i2 =-1’
Veja no exemplo abaixo:
Observe que o valor de delta =-4, e não podemos extrair a raiz de um número negativo, como ‘i2 =-1’ podemos então usar o artifício e trocar o valor -4 por 4i2 t, poderemos então extrair a raiz de ‘4i2 =-4’
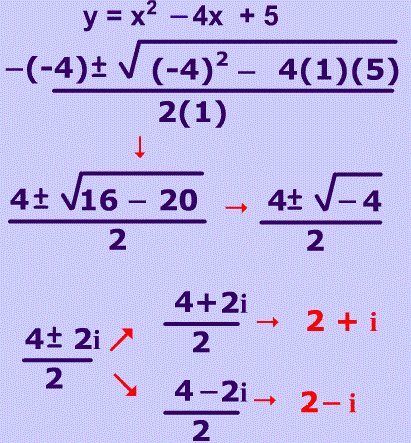
Equação do 2 grau com delta negativo!
Como Resolver Equação do 2º grau
2) Método da Soma e Produto
Algumas questões é perguntado o valor da SOMA e do PRODUTO das raízes da equação. Quando for uma equação do segundo grau podemos usar uma técnica bem simples para calcular as raízes da função. Mas você deverá treinar muito antes de usar somente essa técnica pois no início ela parecerá ser bem difícil, mas depois que você se acostumar com ela não vai querer mais usar a Bháskara.
Toda função do segundo grau, que tenha raízes x’= r1 e x” = r2
Pode ser escrita na forma fatorada:
ax² + bx + c = 0 fica na forma fatorada assim:
Aplicando a distributiva temos:
f(x)=a⋅(x2−r2x−r1x+r1r2)
Colocando o x em evidência temos:
f(x)=a⋅(x2−x (r2 + r1)+r1r2)
f(x)=a⋅(x2− (r2 + r1)x+r1r2)
No caso do termo independente “c”, temos que ele é o produto das raízes (r1.r2) multiplicado por “a”. Portanto, também para o produto, usamos uma fórmula:
f(x)=a⋅(x2− (r2 + r1)x+r1r2)
Se a = 1 temos que a soma das raízes = “-b” e o produto é “c”
Se o valor de a =1, podemos escrever x² + bx + c como
Como Resolver Equação do 2º grau
Fórmula da Soma e produto para a=1:
x² – Sx + P= 0
Logo o coeficiente “b” nada mais é do que será a SOMA DAS RAÍZES (r1+r2), multiplicado por “-1” e o PRODUTO DAS RAÍZES (r1 . r2), SERÁ O TERMO INDEPENDENTE C
Exemplos:
|
f(x) = x2 – x – 2 |
Se a soma é
r2 + r1 = 1 e o produto é r1 . r2 = -2 as raízes serão: 2 e -1 |
|
f(x) = 2x2 – 4x – 16 |
Se a soma é r2 + r1 = -b/a = 2
e o produto é r1 . r2 = c/a = -16/2 =-8 as raízes serão: 4 e -2 |
|
f(x) = 2x2 + 8x |
Se a soma é
r2 + r1 = -b/a = 8/2 = 4 e o produto é r1 . r2 = c/a = 0/2 = 0 as raízes serão: 0 e -4
|
|
f(x) = x2 – 25 |
Se a soma é
r2 + r1 = -b/a = 0/1 =0 e o produto é r1 . r2 = c/a = -25/1 =-25 as raízes serão: 5 e -5 |
|
f(x) = x2 – 5x |
Soma = -(b)/a = -(-5)/1 =-5
Produto = c/a =0/1 =0 as raízes serão: 0 e 5 |







.jpg)







