Contents
- 1 Estatística no ENEM
- 2 Variância e Desvio Padrão
- 2.1 Soma dos quadrado dos desvios
- 2.2 Aulas no nosso canal do YouTube
- 2.3 [Aula 1] Estatística – Média, Moda e Mediana (Parte 1)
- 2.4 [Aula 2] Estatísticas – Desvio Padrão e Variância
- 2.5 [Aula 3] Resoluções – Estatística (Parte 1)
- 2.6 [Aula 4] Resoluções – Estatística (Parte 2)
- 2.7 VARIÂNCIA
- 2.8 V = 32,8 /5 = 6,56
- 2.9 DESVIO PADRÃO
- 2.9.1 É a raiz quadrada da variância
- 2.9.1.1 Pratique esse conceito resolvendo essa questão:
- 2.9.1.2 Exemplo – Calcular a média, variância e o desvio padrão de um aluno que apresentou as notas:
- 2.9.1.3 A (9, 9, 9, 1, 1, 1) e um aluno B (8, 8, 8, 2, 2, 2) qual é o aluno de melhor desempenho?
- 2.9.1.4 Veja que ao calcular as médias os dois alunos empataram no quesito (média 5 para ambos), mas para o cálculo do desvio padrão, o aluno B teve o menor resultado, por isso foi melhor classificado. O aluno B teve um afastamento 3 pontos em relação a média e o aluno A de 4 pontos. Por isso teremos um resultado de avaliação melhor para o aluno B.
- 2.9.1.5 Lembre-se: quanto menor o Desvio padrão de suas notas melhor o aluno!
- 2.9.1.6
- 2.9.1 É a raiz quadrada da variância
Estatística no ENEM
Variância e Desvio Padrão
Em Junho publiquei um post que ensinava a calcular Moda, Média e Mediana (para ver clique aqui ). Esse assunto volta a tona pois estamos a poucos dias da prova do ENEM e certamente teremos no mínimo 2 questões que envolve o assunto de estatística.
Dando continuidade a este assunto citado no post de junho ( clique aqui ), além da moda, mediana e desvio o ENEM cobra em sua prova Variância e Desvio Padrão.Em Probabilidade e Estatística, o desvio padrão é a medida mais comum da dispersão estatística ( e é representado pelo símbolo sigma, σ). Um baixo desvio padrão indica que os dados tendem a estar próximos da média; um desvio padrão alto indica que os dados estão espalhados por uma gama de valores. Em outras palavras um baixo desvio padrão deixa um candidato que concorre a uma vaga, por exemplo, melhor colocado em relação ao seu concorrente, caso estejam tecnicamente empatados no quesito média.
Então vamos aprender a calcular o desvio padrão que é a raiz quadrada da variância.
MÉDIA
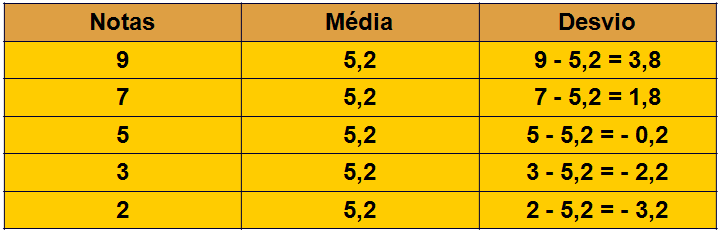
João fez 5 provas e suas notas foram: 9,7,5,3, e 2. Quanto foi a média de João no último bimestre?
Média: (9 + 7 + 5 +3 + 2)/5 = 5,2
Voltando ao exemplo das notas de João, podemos calcular o desvio, que é a diferença de cada nota em relação à média:
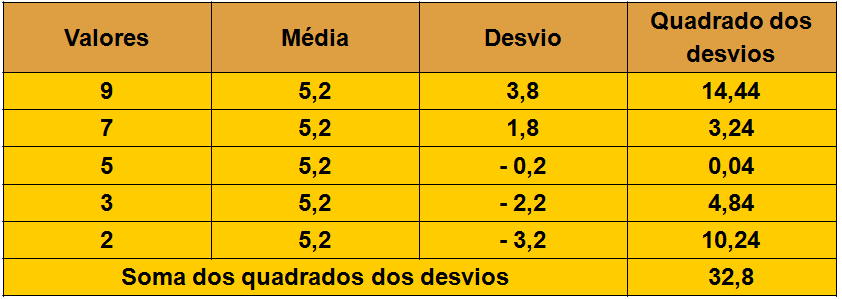
Soma dos quadrado dos desvios
Outro dado importante em estatística é obtido pela soma dos desvios ao quadrado. Cada desvio é elevado ao quadrado e, em seguida, somados
Aulas no nosso canal do YouTube
[Aula 1] Estatística – Média, Moda e Mediana (Parte 1)
[Aula 2] Estatísticas – Desvio Padrão e Variância
[Aula 3] Resoluções – Estatística (Parte 1)
[Aula 4] Resoluções – Estatística (Parte 2)
VARIÂNCIA
A soma dos quadrados dos desvios dividida pelo número de ocorrências é chamada de variância. Logo:
V = 32,8 /5 = 6,56
DESVIO PADRÃO
É a raiz quadrada da variância
Pratique esse conceito resolvendo essa questão:
Exemplo – Calcular a média, variância e o desvio padrão de um aluno que apresentou as notas:
A (9, 9, 9, 1, 1, 1) e um aluno B (8, 8, 8, 2, 2, 2) qual é o aluno de melhor desempenho?
Veja que ao calcular as médias os dois alunos empataram no quesito (média 5 para ambos), mas para o cálculo do desvio padrão, o aluno B teve o menor resultado, por isso foi melhor classificado. O aluno B teve um afastamento 3 pontos em relação a média e o aluno A de 4 pontos. Por isso teremos um resultado de avaliação melhor para o aluno B.
Lembre-se: quanto menor o Desvio padrão de suas notas melhor o aluno!
Abraço e boa prova!


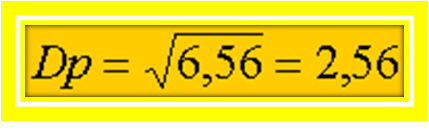


![Gráfico da Função Exponencial [vídeo] 4 gráfico função exponencial](https://geniodamatematica.com.br/wp-content/uploads/2016/10/grafico-função-exponencial.png)