Resolução Prova FUVEST 2020

Veja aqui todas as questões e a resolução prova FUVEST 2020 

Questão 13

Carros que saem da cidade A rumo a alguma das cidades turísticas E, F e G fazem caminhos diversos, passando por pelo menos uma das cidades B, C e D, apenas no sentido indicado pelas setas, como mostra a figura. Os números indicados nas setas são as probabilidades, dentre esses carros, de se ir de uma cidade a outra.

Nesse cenário, a probabilidade de um carro ir de A a F é

(A) 0,120.

(B) 0,216.

(C) 0,264.

(D) 0,336.

(E) 0,384.

Questão 13 Resolvida

Temos 3 caminhos possíveis para sair de A e chegar em F, São eles: ACF, ABCF e ABDF.

Para calcular a probabilidade  dos caminho referidos, precisamos efetuar os seguintes produtos:

ACF = 0,2 X 0,6 = 0,12

ABCF = 0,8 x 0,1 x 0,6 = 0,048

ABDF = 0,8 x 0,9 x 0,3 = 0,216

Agora é só somar as probabilidades de todos os caminhos possíveis, saindo de A e chegando em F. 

Total = P(ACF) + P(ABCF) + p(ABDF) = 0,12 + 0,048 + 0,216 = 0,384

Resposta da Questão 13: E

Questão 14

Se, em 15 anos, o salário mínimo teve um aumento nominal de 300% e a inflação foi de 100%, é correto afirmar que o aumento real do salário mínimo, nesse período, foi de

(A) 50%.

(B) 100%.

(C) 150%.

(D) 200%.

(E) 250%.

Questão 14 Resolvida

Vamos pressupor que o salário S aumentou 300%.

Sabendo que a taxa “i” é 300% = 300/100 = 3 e usando a relação de acréscimo temos, após o aumento, o valor de:

S_Aumento = S (1 + i) = S(1 +3) =  4S

Também ocorreu o aumento de inflação com uma taxa i de  100% = 100/100 = 1, ou seja S_inflação = S(1 + 1) = 2S. Nesse caso a inflação retira o poder de compra e deverá ser diminuída no calculo do ganho real. Logo o salário real, após essas duas correções fica:

S_Real = S_Aumento – S_inflação = 4S – 2S = 2S

2.S representa o dobro do salário ou seja, ele teve um aumento de 100% 

Resposta da Questão 14: B

Resolução Prova FUVEST 2020

Questão 15

O cilindro de papelão central de uma fita crepe tem raio externo de 3 cm. A fita tem espessura de 0,01 cm e dá 100 voltas completas. Considerando que, a cada volta, o raio externo do rolo é aumentado no valor da espessura da fita, o comprimento total da fita é de, aproximadamente,

(A) 9,4 m.

(B) 11,0 m.

(C) 18,8 m.

(D) 22,0 m.

(E) 25,1 m.

Note e Adote:
π = 3,14

Questão 15 Resolvida

Sabemos que o comprimento de cada uma das 100 voltas é calculado por C = 2.π.R, mas cada uma dessas voltas terá um raio diferente, comum acréscimo de 0,1. Dessa forma teremos uma PA de 100 termos de razão 0,1, onde cada um dos termos é calculado pelo comprimento das circunferências obtidas:

PA (  C₁, C₂,  C₃,  … , C₁₀₀)

PA ( 2.π.R₁, 2.π.R₂, 2.π.R₃, …, 2.π.R₁₀₀),

Observe que o comprimento total C_Total da fita é dado pela soma de todas os comprimentos de cada volta:

C_Total  = (2.π.3,01 + 2.π.3,02 + 3.π.3,03 + …. + 2.π.3,04)

C_Total  = 2.π(3,01 + 3,02 + 3,03 + …4)

Usando a formula da PA, onde o a1 = 3,01; an = 4  e n =100 temos:

S =(a1 +an).n/2 = (3,01 + 4).100/2 = 7,01.50 = 350,5

Substituindo na expressão: C_Total  = 2.π(3,01 + 3,02 + 3,03 + …4)

C_Total  = 2.π(350,5) =2.3,14.350,5 = 2201,14 cm = 22,01 m

Resposta da Questão 15: D

Resolução Prova FUVEST 2020

Questão 161

Um objeto é formado por 4 hastes rígidas conectadas em seus extremos por articulações, cujos centros são os vértices de um paralelogramo. As hastes movimentam-se de tal forma que o paralelogramo permanece sempre no mesmo plano. A cada configuração desse objeto, associa-se d, a medida do menor ângulo interno do paralelogramo. A área da região delimitada pelo paralelogramo quando d = 90° é A.

Para que a área da região delimitada pelo paralelogramo seja  o valor de  é necessariamente, igual a:

(A) 15°

(B) 22,5°

(C) 30°

(D) 45°

(E) 60°

Resolução Comentada

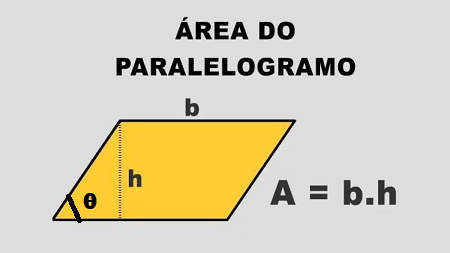
A área de um retângulo é A = b. h onde b = base e h = altura. Para que essa área seja reduzida a altura deveremos ter:

A = b.h/2 = b.h.sen30⁰ 

Como senθ = sen 30^o = 1/2  logo θ = 30

Resposta da Questão 16: C

Questão 17

A menor esfera na qual um paralelepípedo reto-retângulo de medidas 7 cm x 4 cm x 4 cm está inscrito tem diâmetro de

(A) 9 cm.

(B) 10 cm.

(C) 11 cm.

(D) 12 cm.

(E) 15 cm.

Resolução Comentada

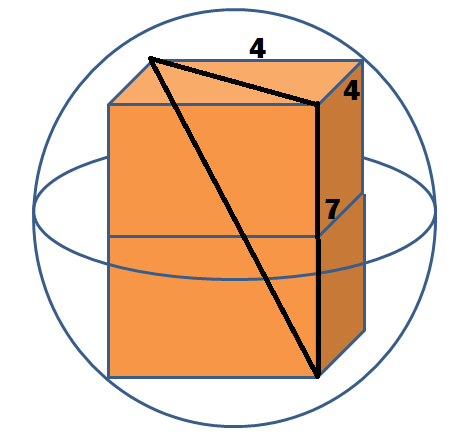
Se o paralelepípedo apresenta os seus vértices tangenciados pela esfera então a diagonal do mesmo será o diâmetro da esfera.

A diagonal do paralelepípedo é calculada por:

D² = a² + b² + c²

D² = 7² + 4² + 4²

D² = 49 + 16 + 16 

D² = 81    >>>>>>> D = 9

logo o diâmetro do paralelepípedo também será igual a 9

Gabarito: A

Questão 18

A dona de uma lanchonete observou que, vendendo um combo a R$ 10,00, 200 deles são vendidos por dia, e que, para cada redução de R$ 1,00 nesse preço, ela vende 100 combos a mais. Nessas condições, qual é a máxima arrecadação diária que ela espera obter com a venda desse combo?

(A) R$ 2.000,00

(B) R$ 3.200,00

(C) R$ 3.600,00

(D) R$4.000,00

(E) R$ 4.800,00

Questão 18 Resolvida

O valor arrecadado na venda é de 10×200 = 2000

Ao diminuir 1,00 R$ há um aumento de 100 combos, logo a relação fica:

Valor Arrecadado = (200 + 100.X).(10 -X)

Valor Arrecadado = 2000 – 200.X + 1000.X -100.X²

Valor Arrecadado = -100.X² + 800.X  + 2000

O valor máximo da função é calculado pelo vértice (Y_v)

Yv = -[b² -4.a.c]/4.a

Yv = -[800² -4.(-100).2000]/4.(-100)

Yv = 640.000 +80000 = 1440000/(-400) = 3.600

Resposta da Questão 18: C

Prova Enem 2020 Resolvida – Matemática

Resolução Prova FUVEST 2020

Questão 19

A função E de Euler determina, para cada número natural n, a quantidade de números naturais menores do que n cujo máximo divisor comum com n é igual a 1. Por exemplo, E (6) = 2 pois os números menores do que 6 com tal propriedade são 1 e 5. Qual o valor máximo de E (n), para n de 20 a 25?

(A) 19

(B) 20

(C) 22

(D) 24

(E) 25

Questão 19 Resolvida

Vamos entender E (6) = 2 ser 1 e 5.

Sabemos que n<6 é 1,2,3,4,5 os únicos números, dessa lista, que apresentam MDC = 1, com o número 6 são os números 1 e 5.

Nossa função descreve que,  os números devem ser menores que n e primos com n. Precisamos retirar os números menores que n que tenham primo em comum com n.

Vamos para n=20: 1, 3, 7, 9, 11, 13, 17 e 19 ou seja E(20) = 8

n=21: 1, 2, 4, 5, 8, 10, 11, 11, 13, 16, 17, 19 3 20   ou seja  E(21) = 12

Vamos direto para o maior número  primo (23), pois nesse caso temos apenas um primo, que é o próprio valor 23.

logo, n=23: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 11, 12,13,14, 15, 16, 17, 18, 19, 20, 21, 22  ou seja  E(23) = 22

Resposta da Questão 19: C

Questão 20

Se 3x² – 9.x + 7 = (x – a)³ – (x -b)³  para todo número real x, o valor de a + b é:

(A) 3.

(B) 5.

(C) 6.

(D) 9.

(E) 12.

Questão 20 Resolvida

Resolução:

3x² – 9.x + 7 = (x – a)³ – (x – b)³

3x² – 9.x + 7 = x³ – 3.x².a +  3.x.a² – a³  – (x³ – 3.x².b +  3.x.b² – b³

3x² – 9.x + 7 = x³ – 3.x².a +  3.x.a² – a³  – x³ + 3.x².b  –  3.x.b² + b³

3x² – 9.x + 7 = (3b -3a).x² + (3.a² – 3.b²).x – a³ + b³

Igualando os polinômios temos:

3.b – 3a = 3

3a² – 3.b² = -9

-a³ + b³ = 7

3(b – a) = 3

3(a² – b²) = -9

– a³ + b³ = 7

b – a = 1 

a² – b² = -3

b³ – a³ = 7

b – a = 1

(a + b).(a – b) = -3

b³ – a³ = 7  

b – a = 1

(a +  b). (-1) = -3

b³ – a³ = 7

b – a = 1

a + b = 3

Chegamos no que é pedido e não precisamos mais continuar resolvendo o sistema: a + b=3.

Resposta da Questão 20: A

Resolução Prova FUVEST 2020

Questão 21

Uma agência de turismo vendeu um total de 78 passagens para os destinos: Lisboa, Paris e Roma. Sabe-se que o número de passagens vendidas para Paris foi o dobro do número de passagens vendidas para os outros dois destinos conjuntamente. Sabe-se também que, para Roma, foram vendidas duas passagens a mais que a metade das vendidas para Lisboa. Qual foi o total de passagens vendidas, conjuntamente, para Paris e Roma?

(A) 26

(B) 38

(C) 42

(D) 62

(E) 68

Questão 21 Resolvida

L + P + R = 78 (equação 1)

P = 2(L + R) = 2L + 2R (equação 2)

R = 2+ (L/2)  (equação 3)

Sendo assim, podemos desenvolver as equações:

L + P + R = 78 (vezes -2)

-2L -2P -2R = -156

2L – P + 2R = 0

———————-

0 -3P + 0 = -156

P = 52 passagens

L + P +  2+ (L/2) = 78

L + 52 +  2+ (L/2) = 78

3L/2 = 24

L = 16 passagens

R = 2 + 16/2 = 10 passagens

Então, o total vendido para Paris e Roma será P + R = 62 passagens

Resposta da Questão 22:  D

Questão 22

Um ponto (x, y) do plano cartesiano pertence ao conjunto F se é equidistante dos eixos OX e OY e pertence ao círculo de equação . 

É correto afirmar que F

(A) é um conjunto vazio.

(B) tem exatamente 2 pontos, um no primeiro quadrante e outro no segundo quadrante.

(C) tem exatamente 2 pontos, ambos no primeiro quadrante.

(D) tem exatamente 3 pontos, sendo dois no primeiro quadrante e outro no segundo quadrante.

(E) tem exatamente 4 pontos, sendo dois no primeiro quadrante e dois no segundo quadrante.

Questão 22 Resolvida

Um ponto equidistante dos eixos OX e OY pertence à reta de equação y = x ou y = – x.

  x² + y² – 2x – 6y + 2 = 0, devemos ter:

O conjunto de pontos que é equidistante dos eixos coordenados é dado pelas retas

y = x

y = -x

  Para o caso y = x ; substituindo na equação x² + y² – 2x – 6y + 2 = 0,

x² + x² – 2x – 6x + 2 = 0,

2x²  – 8x  + 2 = 0,

calculando as raízes temos: 

x´= 2 + √3   e x´´= 2 – √3  

temos dois pontos pois y = x

y = x >>> (2 + √3  ; 2 + √3  )   e (2 – √3 ; 2 – √3 )

Agora vamos calcular os pontos para y = -x 

x² + y² – 2x – 6y + 2 = 0,

x² + (-x)² – 2x – 6(-x) + 2 = 0,

2x² + 4x + 2 = 0,    calculando as raízes temos x´=  x´´= -1 

Se y = -x >>> (-1; -1)

Temos aqui um ponto no 2^o quadrante num total de 3 pontos, dois no primeiro quadrante e um no segundo quadrante, o que poderia indicar a alternativa d) como nosso gabarito.

Mas como no enunciado temos um círculo, no enunciado, nos leva a ideia de área cercada pela circunferência. Como uma das retas (y=x) é secante à circunferência, teríamos infinitos pontos pertencentes ao conjunto F, não só os 3 que achamos.

A equação do enunciado, não é referente a um círculo e sim uma circunferência. Dessa forma a questão é passível de anulação

Gabarito: Questão anulada

Questão 23

Uma cidade é dividida em dois Setores: o Setor Sul, com área de 10 km2, e o Setor Norte, com área de 30 km2. Após um final de semana, foram divulgados os seguintes totais pluviométricos:

É correto afirmar que o total pluviométrico desse final de semana na cidade inteira foi de

(A) 15 mm.

(B) 17 mm.

(C) 22 mm.

(D) 25 mm.

(E) 28 mm.

Questão 23 Resolvida

A média aritmética ponderada é calculada multiplicando cada valor do conjunto de dados pelo seu peso.  Depois, encontra-se a soma desses valores que será dividida pela soma dos pesos.

O total pluviométrico do final de semana no Sul foi (7 + 9)mm = 16mm

O total pluviométrico do final de semana no Norte foi (11 + 17)mm = 28mm

O total pluviométrico do final de semana, em mm, na cidade foi :

(16.10 + 28.30)/(10+30) = 160+840/40

Total = 1000/40 = 25 mm

Resposta da Questão 23: D

Questão 24

As possíveis soluções, em polegadas (inches, em inglês), para o problema matemático proposto no quadrinho, no caso em que os pontos A, B e C estão em uma mesma reta, são

(A)  e 10

(B) , 5 e 10

(C)  e 10

(D)  e 10

(E)  e 5

Questão 24 Resolvida

Temos pelo enunciado a relação entre as distâncias:

d_AC = 2.d_AB

Sabendo-se que A, B e C são colineares, temos a formação de seguinte reta:

Dessa forma, seguindo as orientações do enunciado, temos:

d_AC = 2.d_AB

x – 0 = 2.(5 – x)

3.x = 10 

x = 10/3;

logo   d_AC = 10/3

Podemos ter um segundo posicionamento para o ponto A:

d_AC = 2.d_AB

x – 0 = 2(x -5) logo x = 10

d_AC = 2.d_AB

d_AC = 10

Logo temos duas respostas para d_AC 

d_AC = 10   e  d_AC = 10/3

Resposta da Questão 24:  A