Resolução da Prova do ITA 2019 – Matemática Resolvida [VÍDEOS]

Mantendo o padrão de sempre a prova de Matemática repetiu o nível elevado de raciocínio lógico de suas questões. Veja aqui a Resolução da Prova do ITA 2019 – Fase 1  (Prova de Matemática corrigida e comentada em vídeos pelo prof. Regis Cortês).

MATEMÁTICA

Notações

R : conjunto dos números reais

i : unidade imaginária i ² = 1

det(M) : determinante da matriz M

M^-1 : inversa da matriz M

M^T : transposta da matriz M

AB : segmento de reta de extremidades nos pontos A e B

[a, b] = {x ε R : a≤x≤b} Observação: Os sistemas de coordenadas considerados são os cartesianos retangulares

Resolução da Prova do ITA 2019

Questão 37.

Considere um retângulo ABCD em que o comprimento do lado AB é o dobro do comprimento do lado BC. Sejam M o ponto médio de BC e N o ponto médio de CM. A tangente do ângulo MÂN é igual a

A( ) 1/35.

B( ) 2/35.

C( ) 4/35.

D( ) 8/35.

E( ) 16/35.

Resolução

α = γ – β 

tgα = tg(γ – β)

tgα = (tgγ -tgβ)/(1+ tgγ.tgβ)

tgβ = cat op/hip

tgβ = x/2  / 2x

tgβ =  1/4

tg γ = (x/2 + x/4) / 2x

tg γ =  (3x/4 )/ 2x 

tg γ =  3/8

tgα = (tgγ -tgβ)/(1+ tgγ.tgβ)

tgα =  (3/8 –  1/4) /(1 + 3/8.1/4)       

tgα =  4/35

RESPOSTA C

(Resolução em vídeo da questão 37)

Resolução da Prova do ITA 2019

Veja aqui o seu curso online Gênio da Matemática,  para passar no ITA, Vestibular e Enem!

Questão 38.

Seja p(x) = x³ + ax² + bx um polinômio cujas raízes são não negativas e estão em progressão aritmética. Sabendo que a soma de seus coeficientes é igual a 10, podemos afirmar que a soma das raízes de p(x) é igual a

A( ) 9.

B( ) 8.

C( ) 3.

D( ) 9/2 .

E( ) 10.

Resolução

P(x) = x³ + ax² + bx

 x³ + ax² + bx = 0

x(x² + ax + b) = 0

x₁ = 0

Raízes (R) estão em PA: (0, r, 2r)

Soma dos coeficientes = 10

1 + a + b = 10

a + b = 9

Relações de Girard

x1 + x2 + x3 = – b/a
x1 . x2 + x1 . x3 + x2 . x3 = c/a
x1 . x2 . x3 = – d/a

x1 + x2 + x3 = – b/a 

0 + r + 2r = – a/1 

a = -3r 

x1 . x2 + x1 . x3 + x2 . x3 = c/a

0.r + 0.2r + r.2r = b/1

2r² = b

a + b = 9

-3r + 2r² = 9

2r² -3r – 9 = 0

r1 = 3   e     r2 = -3/2 (não válida)

a = -3r = -3.3 = -9 

b = 2r2 = 2.32 = 18

P(x) = x³ + ax² + bx

P(x) = x³ – 9x² + 18x

S = -b/a = -(-9)/1 = 9

RESPOSTA A

(Resolução em vídeo da questão 38)

Resolução da Prova do ITA 2019

Questão 39.

Seja a circunferência de equação x² + y² = 4. Se r e s são duas retas que se interceptam no ponto P = (1, 3) e são tangentes a , então o cosseno do ângulo entre r e s é igual a

A( ) 1/5 .

B( ) √7/ 7 .

C( ) 1/2 .

D( ) √2/2 .

E( ) 2√6/5 .

(x – xo)² + (y – yo)² = R²

x² + y² = 2²

C(0,0) e R=2

α=2θ

cos2θ = cos²θ – sen2θ

sen²θ + cos²θ = 1

cos²θ = – sen²θ + 1

cos²θ = – sen²θ + 1- sen2θ

Senθ= co/hip

Senθ= Raio/h

Senθ= 2/√10

h²=3²+1²

h=√10

cos2θ = 1 – 2.(2/√10)²

cos2θ = 1 – 2.4/10

cos2θ = 1/5

RESPOSTA A

(Resolução em vídeo da questão 39)

Resolução da Prova do ITA 2019

Questão 40.

A superfície lateral de um cone circular reto corresponde a um setor circular de 216, quando planificada. Se a geratriz do cone mede 10 cm, então a medida de sua altura, em cm, é igual a

A( ) 5.

B( ) 6.

C( ) 7.

D( ) 8.

E( ) 9.

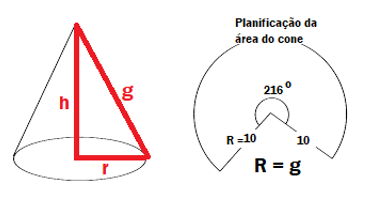
C = 2π.R

C =α.R

π rad————-180⁰

X rad————-216⁰

X = 216⁰ . π/180⁰

X = 1,2.π

C = 1,2π.10

C = 12π

C = 2π.r

12π = 2π.r

r = 6

g² = h² + r²

10^₂ = h² + 6²

h = 8                          RESPOSTA D

(Resolução em vídeo da questão 40)

Questão 41.

Assinale a opção que identifica o lugar geométrico de todos os pares ordenados (a, b)∈R² que tornam impossível o sistema linear

S :

A( ) Uma elipse

B( ) Uma reta

C( ) Uma parábola

D( ) Uma hipérbole

E( ) Um único ponto

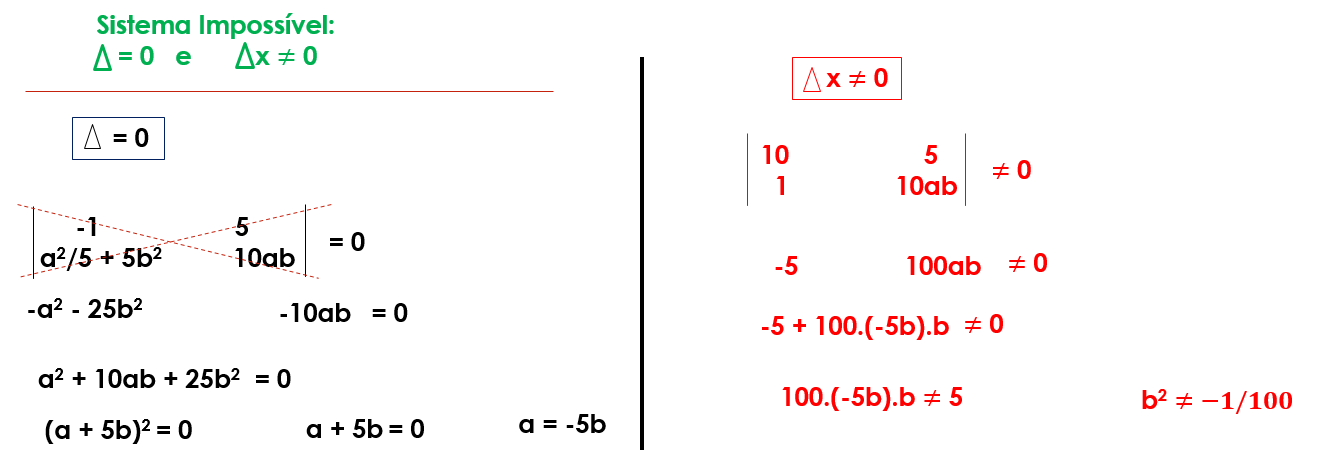
 RESPOSTA D

(Resolução em vídeo da questão 41)

Resolução da Prova do ITA 2019

Baixe aqui as provas dos anos anteriores: Link

Questão 42.

Sabe-se que -2+2i é uma das raízes quartas de um número complexo z. Então, no plano de Argand-Gauss, a área do triângulo, cujos vértices são as raízes cúbicas de z, é igual a

A( ) 4(√3 + 1).

B( ) 6 √3.

C( ) 8(√3 1).

D( ) 10√3.

E( ) 12√3.

Resolução W = – 2 + 2i  e Z = W⁴

ρ²= 2² + 2²

ρ= 2√2

z = (– 2 + 2i)⁴ =

[(2√2)⁴ (cos4.135° + i . Sen4.135°)=

Z = 64 . (cos 540° + i . sen 540°) =

Z = 64 . (cos 180° + i . sen 180°)

0≤k ≤n-1

0≤k ≤2

Raízes Cúbicas de Z:

k=0

Z1= 4. (cos60⁰ + i.sen60⁰)

Z1= 2 + 2.√3.i

Z2= 4. (cos180⁰ + i.sen180⁰)

k=2

Z3= 4. (cos300⁰ + i.sen300⁰)

Z3= 2 – 2.√3.i

A =B.h/2 =  4√3.6/2 = 

A = 12√3

Questão 43.

Considere as seguintes afirmações:

I. se n é um número natural, então 1/(n + 1) + 1/(n + 2) + ··· + 1/2n≥1/2 .

II. se x é um número real e x³ + x +1=0, então x² + 1/x + 1/x⁶ = 0.

III. se a, b e c são números reais positivos que formam, nessa ordem, uma progressão aritmética, então 1/(√ b + √c) , 1/(√c + √a) , 1/√a + √b) formam, nessa ordem, uma progressão aritmética. É(são) VERDADEIRA(S)

A( ) apenas I.

B( ) apenas I e II.

C( ) apenas I e III.

D( ) apenas II e III.

E( ) todas

I  – VERDADEIRO

Soma da P.A. ≥1/2

(a1+an).n/2 ≥ 1/2

[1/(n+1) + 1/2n].n/2  ≥ 1/2

6n + 2  ≥4n + 4

2n ≥ 2        n ≥ 1

II – FALSO

Parte 1

1 e -1 não são raízes  de x³ + x +1 = 0  pois:

1³ + 1 +1 ≠ 0      e       (-1)³ + (-1) +1 ≠ 0

Parte 1 – VERDADEIRO

x³ + x +1 = 0

x³ + 1 = -x

Parte 2

x² + 1/x + 1/x⁶ =0

(x⁸ + x⁵ + 1)/x⁶ =0

Colocando em evidência a parte azul  (x⁵(x³ + 1) + 1)/x⁶ =0

Substituindo o valor encontrado da parte 2 onde: x³ + 1 = -x

(x⁵(-x) + 1)/x⁶ =0

 (-x⁶ + 1)/x⁶ =0

-1 + 1/ x⁶ = 0

Para -1 + 1/ x⁶  ser = 0, devemos ter 1/ x⁶  = 1 e isso é impossível!

III – VERDADEIRO

PA – Termo médio é a média

aritmética de seus equidistantes:

a₂ = (a₁ + a₃)/2

Logo      2a₂ = a₁ + a₃

2.1/(√c + √a) = 1/(√b + √c) + 1/(√a + √b)

2/(√c + √a)  =  1/(√b + √c)   + 1/(√a + √b)

2/(√c + √a)  =   

 2/(√c + √a) = 2/(√c + √a)

Resolução em vídeo-Questão 43

Resolução da Prova do ITA 2019

Questão 44.

As faces de dez moedas são numeradas de modo que: a primeira moeda tem faces 1 e 2; a segunda, 2 e 3; a terceira, 3 e 4, e assim sucessivamente até a décima moeda, com faces 10 e 11. As dez moedas são lançadas aleatoriamente e os números exibidos são somados. Então, a probabilidade de que essa soma seja igual a 60 é

A( ) 63/128.

B( ) 63/256.

C( ) 63/512.

D( ) 189/512.

E( ) 189/1024.

1) Menor soma possível: 1 + 2 + 3 +…+ 10 = 55
2) Existe uma única maneira da soma ser 55 que é considerar, em cada moeda, sempre o menor valor.

3) Virando apenas uma dessas 10 moedas a soma dá 56.  Número de eventos: C10,1 = 10 vezes.

4) Virando duas moedas a soma dá 57.  Número de eventos: C10,2 = 45 vezes

5) Virando três moedas a soma dá 58.  Número de eventos:  C10,3 = 120

6) E assim sucessivamente até virar todas as moedas gerando o maior valor possível: 2 + 3 + 4…+ 11 = 65

7) Queremos soma 60  – Temos que virar 5 moedas. Número de eventos: C10,5 = 252

8) O número total de resultados possíveis é
C10,0 + C10,1 + C10,2 + C10,3 + … + C10,10 = 1024

9) A probabilidade de que essa soma seja igual a 60 é

252/1024 = 63/256

GABARITO: B

Resolução em vídeo – Questão 44

Resolução da Prova do ITA 2019

Questão 45.

Considere as seguintes afirmações a respeito de matrizes A de ordem n x n inversíveis, tais que os seus elementos e os de sua inversa sejam todos números inteiros:

I. | det(A)| = 1.

II. A^T = A^-1.

III. A + A^-1 é uma matriz diagonal.

É(são) sempre VERDADEIRA(S)

A( ) apenas I.

B( ) apenas III.

C( ) apenas I e II.

D( ) apenas I e III.

E( ) todas.

Resolução

det A = D

det A^-1 = 1/D

Para que a Matriz A e sua inversa tenha valores inteiros, então D=1 ou D=-1

I. | det(A)| = 1.                Verdadeiro

Exemplo:

II   A^t  ≠ A^-1         Falso

III. A + A^-1 é uma matriz diagonal.     Falso

Resolução em vídeo – Questão 45

Questão 46.

Seja f : [-1, 1]→ [-π/2, π/2]a função definida por f(x) = arcsen(x). Então, a soma

é igual a

A( ) 253π/162.

B( )245π/162 .

C( ) -152π/81 .

D( ) -82π/81 .

E( ) -79π/162 .

Resolução 

n=0

f(cos(2Л/3⁰)= arc sen(cos2Л)= arc sen(1)= Л/2

n=1

f(cos(2Л/3¹) = arc sen(-1/2)= –Л/6

n=2

f(cos(2Л/3²) = f(cos(2Л/9) = arc sen(sen(Л/2 – 2Л/9)) = 5Л/18

n=3

f(cos(2Л/3³) = f(cos(2Л/27) = arc sen(sen(Л/2 – 2Л/27)) = 23Л/54

n=4

f(cos(2Л/3⁴) = f(cos(2Л/81) = arc sen(sen(Л/2 – 2Л/81)) = 77Л/162

= Л/2 + (-Л/6) + 5Л/18 + 23Л/54 + 77Л/162 = 245 Л/162

Resolução em vídeo – Questão 46

Resolução da Prova do ITA 2019

Questão 47.

Os volumes de um tronco de cone, de uma esfera de raio 5 cm e de um cilindro de altura 11 cm formam nessa ordem uma progressão aritmética. O tronco de cone é obtido por rotação de um trapézio retângulo, de altura 4 cm e bases medindo 5 cm e 9 cm, em torno de uma reta passando pelo lado de menor medida. Então, o raio da base do cilindro é, em cm, igual a

A( ) 2 √2.

B( ) 2√3.

C( ) 4.

D( ) 2 √5.

E( ) 2 √6.

Resolução

Resolução da Prova do ITA 2019

Resolução em vídeo – Questão 47

Questão  48.

Considere as seguites afirmações:

I. se x1, x2 e x3 são as raízes da equação x³ -2x² + x +2=0, então y1 = x2.x3, y2 = x1.x3 e y3 = x1.x2 são as raízes da equação y³ – y² – 4y – 4 = 0.

II. a soma dos cubos de três números inteiros consecutivos é divisível por 9.

III. √(3 +√5)/2 = (1 + √5)/2 .

É(são) VERDADEIRA(S)

A( ) apenas I.

B( ) apenas II.

C( ) apenas III.

D( ) apenas II e III.

E( ) todas.

I. Sabendo que x₁; x₂; x₃ são as raízes da equação x³ – 2x² + x + 2 = 0, pelas relações de Girard, temos:

ax³ + bx² + cx + d =0

x₁+x₂+x₃ = – b/a
x₁.x₂ + x₁.x₃ + x₂.x₃ = c/a
x₁.x₂.x₃ = – d/a

x³ – 2x² + x + 2 =0

x₁+x₂+x₃ =  -(-2)/1 = 2

x₁.x₂ + x₁.x₃ + x₂.x₃ = 1/1 = 1

x₁.x₂.x₃ = -2/1 = –2

ay³ + by² + cy + d =0

y³ – y² – 4y – 4 =0

y1+y2+y3 = – b/a

y1.y2 + y1.y3 + y2.y3 = c/a

y1.y2.y3 = – d/a

x₂.x₃  + x₁.x₃  + x₁.x₂  = – b/a  = 1

x₂.x₃ . x₁.x₃   + x₂.x3. x₁.x₂+ x₁.x₃ . x₁.x₂ = c/a =-4

x₂.x₃ . x₁.x₃ . x₁.x₂  = – d/a = 4

x₁.x₂. x₃  ( x₁+x₂+x₃ ) = -2.2 = -4

x₁.x₃.x₂.x₁.x₂.   = – d/a = 4

(x₁.x₃.x₂)²   = (–2)2 = 4       

(Verdadeiro)  y_1, y₂ e y₃ são as raízes da equação y³ – y² – 4y – 4 = 0

II) Sejam, x – 1,  x  e  x + 1 são números inteiros e consecutivos.
A soma dos cubos desses números é

(x – 1)³ + x³ + (x + 1)³ =
= x³ – 3x² + 3x – 1 + x³ + x³ + 3x² + 3x + 1 =
= 3x³ + 6x

Sendo a ∈ Z, a soma 3a³ + 6a é divisível por 9, pois por substituição:

3.1³ + 6.1 = 9 ;  3.2³ + 6.2 = 36 ;    3.33 + 6.3 = 99 ;  …. todos são divisíveis por 9

Outra solução:
3a³ + 6a = 3a(a² + 2) = 3a(a² – 1 + 3) =
= 3a(a² – 1 + 3) = 3a[(a + 1)(a – 1) + 3] =
= 3a(a + 1)(a – 1) + 9a e a(a + 1)(a – 1) é múltiplo de 3
(Verdadeiro)

Elevando ao quadrado os dois membros temos:

(3 + √5)/2 = (1 + 2√5 + 5)/4

(3 + √5)/2 =  (6 + 4√5)/4

(3 + √5)/2 = (3 + √5)/2 

Verdadeiro
Assim, as três afirmações são verdadeiras.

GABARITO: E

Resolução em vídeo – Questão 48