Prova Resolvida de Matemática UFRGS 2017

Prova Resolvida de Matemática UFRGS 2017

Prova comentada! Temos aqui a prova resolvida de Matemática UFRGS 2017 ,  para você tirar todas as suas dúvidas!

Baixe a prova aqui:

Questão 26. (B) – Prova Comentada de Matemática UFRGS 2017

Sendo 1cm³ = 10^-6 m³    e     1km³ = 10⁹m³  temos:

10^-6 m³    ___________    0,92 g

96,10⁹ m³     ___________   x             x=8,83.10¹⁶ g  =  8,832.10¹³ kg

Questão 27. (A) Resolução da Prova de Matemática UFRGS 2017

Para resolver essa questão atribuiremos valores aleatórios:

I) (V) Se a < b então – a > -b        a= 1   e   b=2    Se 1 < 2 então – 1 > -2

II) (F) Se a > b então 1/a < 1/b     a=1  e  b=-2    Se 2 > 1 então  1/1 < 1/(-2)

III) (F) Se a < b então a ² < b ²       a=-2   e b=1    Se -2 < 1 então (-2) ² < 1 ²

Questão 28. (C) Resolução da Prova de Matemática UFRGS 2017

I) (V) (1- 2i )(1 + 2i) = 5,          1 – 4i²  = 1+4 =5

II) (V) 2º + 2^-1 + 2^-2 + 2^-3 + … = 2 S =a₁/(1-q)  = 1/(1-1/2) = 2

III) (F)  1 – 2 + 3 – 4 + 5 – 6 + … + 99 – 100 = 50

(1 + 3 + 5 +  …  +99)    S=(a₁+a_n).n/2 = (1+99)50/2 = 2500

(-2 + (-4) + (-6) + … + (-100) )      S=(a₁+a_n).n/2 = (-2 + (-100)).50/2 = -2550

1 – 2 + 3 – 4 + 5 – 6 + … + 99 – 100 = 2500 + (-2550) = -50

 Clique Aqui e Saiba Como Fazer Nossos Grupos de

Questão 29. (E) Resolução da Prova de Matemática UFRGS 2017

Dados:  x – y = 2   e   x ² + y ² = 8,    então x ³ – y³

Sendo  x ³ – y³  = (x – y).(x² + xy + y² )

x ³ – y³  = 2 . (8 + 2) = 20

Questão 30. (B) – Prova Resolvida de Matemática UFRGS 2017

      A primeira sequência (primeira ordem) temos:   (3, 6, 10, 15, …)

Na sequência de segunda ordem, pela diferença dos termos:  PA (3, 4, 5,…)

O valor do número de quadrados da etapa 100  =  a₁(primeira ordem)  +  S₉₉ (segunda ordem)

a₉₉ = a₁ + (n-1).r = 3 + (99 – 1).1 = 101

S₉₉ = (a₁ + a_n).n/2 = (3 + 101).99/2 = 5148

R =  a₁(primeira ordem)  +  S₉₉ (segunda ordem) = 3 + 5148 = 5151

Questão 31. (D) – Prova Comentada de Matemática UFRGS 2017

Regra de três:    Pelo gráfico o crescimento foi de 600 para 6000. Houve um aumento de 5400

600  ______________   100%

5400  ______________    x   x=900%

Questão 32. (C) Prova Resolvida de Matemática UFRGS 2017

Área do quadrado =  Área do triângulo

L2 = B.H/2

x²= (10 − ) . x / 2

2x² = 10x − x²

3 x² – 10x =0

x = 10/3

Questão 33. (B) Prova Resolvida de Matemática UFRGS 2017

O maior triângulo, formado pela união dos pontos médios do quadrado maior, tem base e altura igual a 1/2.

A1 = B . H / 2 = (1/2 . 1/2 ) / 2 = (1/4) /2 = 1/8

A2 = 1/16  , A3 = 1/32 …

PG (1/8, 1/16, 1/32,…) A soma das infinitas áreas é:

S = a1/(1 – q)   = 1/8 /(1 – 1/2) =

S = 1/4

Questão 34. (A) Resolução da prova de matemática UFRGS 2017

log₅X = 2        X = 5² = 25

log₁₀Y = 4     Y = 10⁴

log₂₀Y/X = M

log₂₀10000/25 = M

20^M = 400

20^M =20²     M = 2

Questão 35. (D) – Prova Comentada de Matemática UFRGS 2017

N = número de bactérias, t = número de horas

N(t) = N₀ · 2^l,5St

Dobrando-se o número inicial de bactérias temos:

40 = 20 · 2^l,5St

2 =  2^l,5St

1,5.t = 1

t = 0,666…h= 0,666.60 = 40 min

Questão 36. (A) – Prova Comentada de Matemática UFRGS 2017

p(x)=x² +2(n+2)x+9n. Se as raízes de p(x) = O serem iguais devemos ter Δ = 0

Δ = 0

(b²-4ac)/2a = 0

((2n + 4)² – 4 . 1 . 9n ) /2.1 = 0

n₁ = 1 e n₂ =4

Prova Resolvida de Matemática UFRGS 2017

Questão 37. (E) – Prova Comentada de Matemática UFRGS 2017

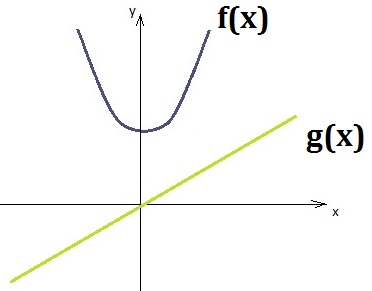
f(x)=x ² +1 e g(x)=x, o intervalo tal que f(x) > g(x)

x² + 1 > x

x² – x + 1 > 0

Aplicando Bháskara temos Δ = -3 , logo essas funções não se encontram. No gráfico a reta está acima da parábola. Isso significa que a reta terá valores de y sempre maiores que a da parábola.

Questão 38. (B) – Prova Comentada de Matemática UFRGS 2017

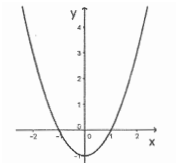
Temos aqui na função   uma translação horizontal para esquerda de 2 unidades, uma translação vertical para cima de 1 unidade e uma dobra entre as raízes -1 e 1, devido a função ser modular. Isso gera o gráfico da letra B.

Prova Resolvida de Matemática UFRGS 2017

Questão 39. (B) – Prova Comentada de Matemática UFRGS 2017

A equação da reta que passa pelos pontos B e D é:

Temos aqui um triangulo equilátero de lado L=1

Retirando-se os 2 pontos do gráfico:

Ponto D (-1,0)

Ponto    B (L/2, L√3/2)      B(1/2, √3/2)

a = (y₂ – y₁)/(x₂ – x₁) = (√3/2 – 0)/(1/2 – (-1)) =  √3/2 / 3/2 =  √3/3

y = a.x + b

0 = √3/3 . (-1) + b

b = √3/3

y = a.x + b

y = √3/3.x + √3/3

Questão 40. (D) – Prova Resolvida de Matemática UFRGS 2017

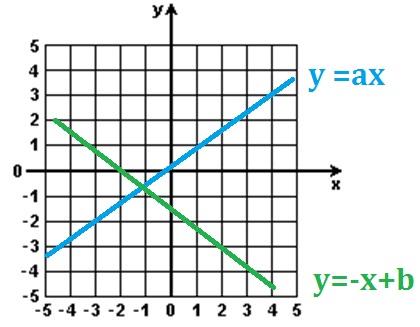
As retas se encontram no ponto de coordenadas negativas, logo isso ocorre no terceiro quadrante.

A reta azul   y = a.x     tem coeficiente linear = 0      e    a > 0

A reta verde  y = -x + b    tem    b < 0    e    angular = -1

Logo a resposta correta é : D pois  a> 0  e b < 0

Questão 41. (B) – Prova Resolvida de Matemática UFRGS 2017

A área da flor é calculada somando a área de um hexágono com mais três círculos ou seis semicírculos.

Hexágono:  A = 6.L²√3/4  = 6. 1²√3/4   = 3√3/2

3 Círculos:   A = 3. π.R²  = 3 c . (1/2)²  = 3.π/4

Somando:

Área total = 3√3/2 + 3.π/4 = 3/2 . (√3 + π/2)

Questão 42. (B) – Prova Resolvida de Matemática UFRGS 2017

Área sombreada = Área do quadrado – (πR²/4+ πR²/4+πr²/4+ πr²/4)

Área sombreada = (R+r)² – (πR²/4+ πR²/4+πr²/4+ πr²/4)

Como o quadrado pode ser inscrito na circunferência maior, sua diagonal é d=L√2 = 1√2 = √2

Então R = √2/2   e    r = 1 – √2/2

Substituindo em A = (R+r)² – (πR²/4+ πR²/4+πr²/4+ πr²/4)

Área sombreada = 1² – (π(√2/2) ²/4+ π(√2/2) ²/4+π(1 – √2/)r²/4+ π(1 – √2/)r²)

Área sombreada = 1 + (√2/2 – 1). π

Questão 43. (B) – Prova Resolvida de Matemática UFRGS 2017

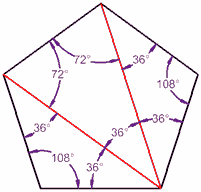
a² = b² + c² – 2.a.b.cos36⁰

(1/2)² = (1/2)² + x² – 2.(1/2).x.cos36⁰

x² – x.cos36⁰ = 0

x = cos36⁰  

Questão 44. (B) – Prova Comentada de Matemática UFRGS 2017

sen 15⁰ = CO / Hip                                cos 15⁰ = CA / Hip

Sen 15⁰ = r /12                                     cos15⁰ = R /12

r =12. Sen 15⁰                                       R = 12.cos15⁰

d = 2.12.Sen 15⁰                                                       D = 2.12.cos15⁰

d = 24.Sen 15⁰                                                          D = 24.cos15⁰

Questão 45. (B) – Prova Resolvida de Matemática UFRGS 2017

VGrande = AB.H =4.3.2 = 24

V_ABCF = Ab.h/3 = (4.2/2).3 /3 =4

V_ABCF = V_AEHF = V_CGFH = V_ACDH = 4

V_AHFC = 24 – 4.4 = 24 – 16 = 8

Questão 46. (A) – Prova Comentada de Matemática UFRGS 2017

A figura é um tetraedro (4 faces triangulares). A soma de todos os lados desses 4 triângulos  é igual a 66. Porém todas as arestas pertencem a 2 triângulos e por isso a soma total é a metade desse valor, ou seja 33.

Questão 47. (E) – Prova Comentada de Matemática UFRGS 2017

Podemos usar Pitágoras, com a medida MN de hipotenusa e os catetos sendo a metade da aresta do cubo.

x² = a² + a²

x = a√2/2

Questão 48. (D) – Prova Resolvida de Matemática UFRGS 2017

Os ângulos são: x, x+70 e (x+70)/2 e sua soma é igual a 180

x + x+7 + (x+70)/2 = 180

x=30

ângulos: 30, 100 e 50

Questão 49. (B) – Prova Comentada de Matemática UFRGS 2017

Temos 10 cartões e 3 deles (marcados com x) apresentam resultados maiores do que 1

Logo a probabilidade é:   P(A) = n(A)/U = 3/10

Questão 50. (B) – Prova Resolvida de Matemática UFRGS 2017

Números de diagonais de um hexágono é C_6,2 – 6. Descontamos 6 pois as arestas não são diagonais.

P(A) = n(A)/U  = (C_6,2 – 6) /  C_6,2  = 9/15 = 3/5