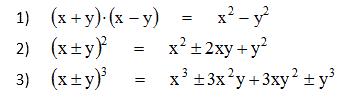Produtos Notáveis Como Você Nunca Viu [Vídeo]

É preciso ficar atento para alguns produtos de binômios, pois eles são muito importantes no desenvolvimento e na estrutura de uma grande parcela de questões de provas de Matemática.
Esses binômios são chamados de produtos notáveis porque:
- Apresentam uma frequência elevada em problemas e provas
- Há um padrão que deve ser “notado” nas questões, e quando detectamos o mesmo e aplicamos suas regras, poupamos muito tempo na resolução.
Neste post, estudaremos os produtos notáveis e suas aplicações nas provas de vestibular e concursos públicos.
1) Quadrado da soma de dois termos: (x + a)2
Dois binômios idênticos, com seus termos separados pelo sinal de +, são conhecidos como quadrados da soma e é representado por: (x + a)2
É preciso memorizar que o quadrado da soma (x + a)2 é igual ao quadrado do primeiro termo, mais duas vezes o primeiro pelo segundo termo, mais o quadrado do segundo termo ou seja:
x2 + 2xa + a2
Logo: (x + a)2 = x2 + 2xa + a2
Exemplo:
Trocando o segundo termo a por 5 temos:
(x + 5)2 = x2 + 2.x.5 + 52= x2 + 10.x + 25
É preciso memorizar toda a estrutura de ida e de volta, ou seja é preciso saber e identificar que:
x2 + 2xa + a2 = (x + a)2 , pois em muitas questões precisamos simplificar polinômios.
Exemplo:
(x2 + 2xa + a2 ) / (x + a) =
(x + a).(x + a) / (x + a) =
(x + a)
2) Quadrado da diferença de dois termos: (x – a)2
Dois binômios idênticos, multiplicados entre si, com seus termos separados pelo sinal de menos (-), são conhecidos como quadrados da diferença e é representado por: (x – a)2
É preciso memorizar que o quadrado da soma (x – a)2 é igual ao quadrado do primeiro termo, menos duas vezes o primeiro pelo segundo termo, mais o quadrado do segundo termo ou seja:
x2 – 2xa + a2
Logo: (x – a)2 = x2 – 2xa + a2
Exemplo:
Trocando o segundo termo a por 7 temos:
(x – 7)2 = x2 – 2.x.7 + 72= x2 – 14.x + 49
É preciso memorizar toda a estrutura de ida e de volta, ou seja é preciso saber e identificar que:
x2 – 2xa + a2 = (x – a)2 , pois em muitas questões precisamos simplificar polinômios.
Exercício
Simplifique a expressão:
(x2 – 10x + 25 ) / (x – 5) =
(x – 5).(x – 5) / (x – 5) =
= x – 5
3) Produto da soma pela diferença de dois termos:
(x + a)(x – a)
Outro produto notável muito comum em provas é esse terceiro caso e o chamamos de Produto da soma pela diferença (x + a)(x – a)
É preciso memorizar que o produto da doma pela diferença de dois binômios
(x + a)(x – a) , é igual ao quadrado do primeiro termo, menos o quadrado do segundo termo. Ou seja:
(x + a)(x – a) = x2 – a2
Logo: (x + a)(x – a) = x2 – a2
Exemplo:
(bz + 8)(bz – 8) = (bz)2 – 82
(bz + 8)(bz – 8) = b2z2 – 64
Exercício
Simplifique a expressão: (3x + 3y)/ (x2 – y2)
(3x + 3y)/ (x2 – y2) = 3(x + y)/(x +y). (x -y)
= 3/(x – y)
4) O Cubo da soma de dois termos: (x + a)3
Neste quarto caso a incidência não é muito grande, ou seja é raro quando aparece esse tipo de produto notável. Mas pode ter a certeza de que o grau de dificuldade é muito grande, pois não estamos muito acostumados a lidar com essa operação.
Neste caso também precisamos “notar” ou seja saber reconhecer a estrutura, pois são são muitas as situações em que precisamos simplificar uma expressão como o cubo da soma
É muito importante memorizar a “fórmula” desta estrutura:
(x + a)3 =(x + a)(x + a)(x + a)
Efetuando a distributiva e somando os termos, chegaremos a seguinte formação deste produto notável:
(x + a)3 = x3 + 3x2a + 3xa2 + a3
Então ao invés de aplicarmos a distributiva podemos atalhar usando a estrutura acima.
Exemplo
(x + 2)3 = x3 + 3.x2.2 + 3.x.22 + 23 = x3 + 6.x2 + 12.x + 8
Exercício
Simplifique a expressão
(x3 + 3x2a + 3xa2 + a3)/(x2 + 2xa + a2) =
(x + a)(x + a)(x + a)/(x + a)(x + a) = (x + a)
5) Cubo da diferença de dois termos: (x – a)3
O cubo da diferença de dois é o produto da diferença entre dois termos de um binômio:
(x – a)3 = (x – a)(x – a)(x – a)
(x – a)3 = x3 – 3x2a + 3xa2 – a3
Exemplo:
(x – 2z)3 = ?
(x – 2z)3 = x3 – 3x22z + 3x(2z)2 – (2z)3
= x3 – 3x22z + 3x4z2 – 8z3
= x3 – 6x2z + 12xz2 – 8z3
Na operação distributiva, todos os termos multiplicam-se entre si:
RESUMO
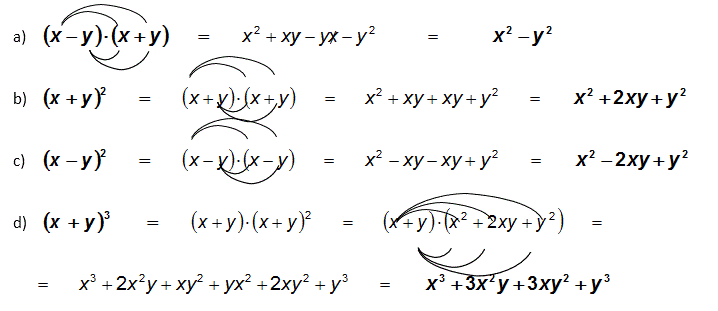
Distributiva produtos notáveis
RESUMO
Há ainda um sexto e sétimo caso de produtos notáveis, mais raro ainda!
Veja abaixo:
6) a³ + b³ = (a + b)(a² – ab + b²)
7) a³ – b³ = (a – b)(a² + ab + b²)
Assista ao Vídeo e faça os exercícios abaixo
EXERCÍCIOS RESOLVIDOS
1) (IMNEC) A diferença entre o quadrado da soma e o quadrado da diferença entre dois números reais é igual a:
a) a diferença dos quadrados dos dois números.
b) a soma dos quadrados dos dois números.
c) a diferença dos dois números.
d) ao dobro do produto dos números.
e) ao quádruplo do produto dos números.
2) Seja x2 + y2 = 60. Qual é o valor positivo de x + y, sabendo que xy = 20?
a) 5
b) 10
c) 15
d) 20
e) 25
3) Desafio
Resolução:
1) (x + y)2 – (x – y)2
x2 + 2xy + y2 – (x2 – 2xy + y2)
x2 + 2xy + y2 – x2 + 2xy – y2
2xy + 2xy
4xy
Resposta E
2) xy = 20
2xy = 2·20
2xy = 40
Somando 40 em ambos os lados da equação e substituindo 40 por 2xy no primeiro membro, teremos:
x2 + y2 = 60
x2 + y2 + 40 = 60 + 40
x2 + y2 + 2xy = 100 voltando nos produtos notáveis:
(x + y)2 = 100
√(x + y)2 = √100
x + y = 10 ou
x + y = – 10