O que mais cai no Enem em Matemática: Funções 2º Grau
Dando continuidade às aulas sobre o que mais cai no Enem em Matemática, falaremos hoje sobre as funções do 2o grau.

Dando continuidade às aulas sobre o que mais cai no Enem em Matemática, falaremos hoje sobre as funções do 2o grau. Lembrando que essa aula complementa o assunto de funções.
O que mais cai no Enem em Matemática
Não perca, toda semana teremos aulas especiais para o Enem.
Veja agora a lista de aulas da sua preparação do ENEM: Link
Caso queira saber mais sobre o Enem: https://geniodoenem.com.br/
Função do 2o Grau
Questão 15 – Sobre o gráfico da função dada por f(x) = – x2 + 6x – 5, é verdade que:
a) sua concavidade é voltada para cima.
b) intercepta o eixo das abscissas para x = – 1.
c) intercepta o eixo das ordenadas para x = – 5.
d) o lucro é máximo para x igual a 4.
e) o lucro é positivo para x entre 2 e 10.
No vídeo abaixo você terá as resoluções das questões desse post!
Questão 16 – O lucro de uma empresa é dado por L(x)= (10 – x)(x – 2 ), onde x é a quantidade vendida. Podemos afirmar que:
a) o lucro é positivo qualquer que seja
b) o lucro é positivo para x maior do que 10.
c) o lucro é NEGATIVO para x igual a
d) o lucro é máximo para x igual a 6.
e) o lucro é negativo para x entre 2 e 10.
Curso Online Gênio da Matemática
Questão 17 – Uma bola lançada verticalmente, para cima, tem sua altura h, em metros, dada em função do tempo t, em segundos, pela equação h = 20t – 5t2. Qual é a altura máxima atingida pela bola em metros?
Questão 18 – Uma bola é largada do alto de um edifício e cai em direção ao solo. Sua altura h em relação ao solo, t segundos após o lançamento, é dada pela expressão h = – 25t2 + 625. Após quantos segundos do lançamento a bola atingirá o solo?
Questão 19 – Sejam R(x) = – 2x2 + 60x e C(x) = 10x + 200 as funções Receita e Custo para certo produto. Para que valores de x o lucro é positivo?
O que mais cai no Enem em Matemática
Questão 20 – O lucro de uma empresa é dado por L(x)= (10 – x)(x – 2 ), onde x é a quantidade vendida. Podemos afirmar que:
a) o lucro máximo é 6.
b) o lucro máximo é 16.
c) o lucro é mínimo para x igual a 16.
d) o lucro é mínimo para x igual a 6.
e) o lucro é negativo para x entre 2 e 10.
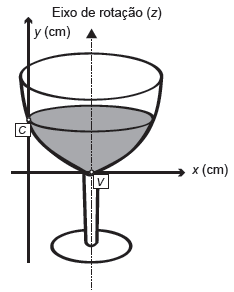
Questão 21 – (Enem) A parte interior de uma taça foi gerada pela rotação de uma parábola em torno de um eixo z, conforme mostra a figura.
A função real que expressa a parábola, no plano cartesiano da figura, é dada pela lei f(x) = 3/2 x2 – 6x + C, onde C é a medida da altura do líquido contido na taça, em centímetros. Sabe-se que o ponto V, na figura, representa o vértice da parábola, localizado sobre o eixo x.
Nessas condições, a altura do líquido contido na taça, em
centímetros, é
A) 1
B) 2
C) 4
D) 5
E) 6
Questão 22 – Qual a altura máxima atingida por um projétil cuja trajetória pode ser descrita pela função: h(x) = – 4x2 + 5, sabendo que h é a altura do projétil e que x é a distância percorrida por ele, em metros?
a) 5 m b) 10 m c) 15 m d) 20 m e) 25 m
O que mais cai no Enem em Matemática
Questão 23 – A respeito do estudo dos sinais de uma função do segundo grau, é possível afirmar, com certeza, que:
a) O valor do discriminante não pode ser usado para determinar a quantidade de raízes reais que uma função do segundo grau possui.
b) Se o valor do discriminante for igual a zero e o coeficiente a for positivo, então todos os pontos dessa função do segundo grau estarão sob o eixo x.
c) Se o valor do discriminante for igual a zero e o coeficiente a for positivo, então todos os pontos dessa função estarão acima do eixo x, exceto pelo vértice que estará sobre esse eixo.
d) Se o valor do discriminante for menor que zero, a função possui duas raízes reais e distintas e outras duas raízes complexas.
e) Se o valor do discriminante for maior que zero, não será possível calcular as raízes dessa função.
Questão 24 – A água é essencial para a vida e está presente na constituição de todos os alimentos. Em regiões com escassez de água, é comum a utilização de cisternas para a captação e armazenamento da água da chuva. Ao esvaziar um tanque contendo água da chuva, a expressão
representa o volume (em m3) de água presente no tanque no instante t (em minutos). Qual é o tempo, em horas, necessário para que o tanque seja esvaziado?
a) 360. b) 180. c) 120. d) 6. e) 3.
Questão 25 – ENEM – Para evitar uma epidemia, a Secretaria de Saúde de uma cidade dedetizou todos os bairros, de modo a evitar a proliferação do mosquito da dengue. Sabe-se que o número f de infectados é dado pela função f(t) = – 2t2 + 120t (em que t é expresso em dia e t = 0 é o dia anterior à primeira infecção) e que tal expressão é válida para os 60 primeiros dias da epidemia.
A Secretaria de Saúde decidiu que uma segunda dedetização deveria ser feita no dia em que o número de infectados chegasse à marca de 1 600 pessoas, e uma segunda dedetização precisou acontecer.
A segunda dedetização começou no
a) 19º dia.
b) 20º dia.
c) 29º dia.
d) 30º dia.
e) 60º dia.
RESPOSTAS
15) D
16) D
17) 20 m
18) 5 s
19) Intervalo: ]5;20[
20) B
21) Resolução:
A parábola corta o eixo x em apenas um ponto. Dessa forma, a função do segundo grau f(x) = 3/2 x2 – 6x + C possui duas raízes reais e iguais. logo o valor de Δ = 0.
Então:
(6)2 – 4.(3/2).c = 0
36 – 6c = 0
6c = 36
c = 6
Resp.: E
22) A
23) C
24) D
25) B
Não perca, toda semana teremos aulas especiais para o Enem.
Veja agora a lista de aulas da sua preparação do ENEM: Link
Caso queira saber mais sobre o Enem: https://geniodoenem.com.br/