Notação Científica e Ordem de Grandeza [Vídeo]

Você sabia que há uma grande diferença entre diferença entre Notação Científica e Ordem de Grandeza?
Notação Científica e Ordem de Grandeza
Vamos entender essa diferença pois esse é um assunto de grande importância, tanto nas provas de Física como na de Matemática. Além disso, cai muito em provas de vestibular e principalmente na do Enem!
Notação Científica e Ordem de Grandeza
Notação Científica
Muitas vezes chegamos na resposta correta, mas essa não poderá ser usada, pois precisará ser escrita de outra forma.
Esse formato se chama notação científica e o mesmo segue algumas regrinhas básicas que vamos comentar agora pra você!
Vamos escolher alguns números aleatoriamente e reescrevê-los em notação científica
Escrevendo os números abaixo de modo que na parte inteira apareça apenas um algarismo, diferente de zero, temos:
56 = 5,6⋅101
789 = 7,89⋅102
2376 = 2,376.103
66.789 = 6,6789.104
Os números acima foram escritos em notação científica. observe que sempre deixamos apenas um algarismo significativo antes da vírgula e os demais algarismos decimais sempre depois da vírgula. Veja também que sempre aparecerá uma base 10 nesse número que foi escrito em notação científica.
Forma de escrever um número N em notação científica:
N = y.10n
Sendo que o valor de “y” deverá pertencer ao intervalo entre 1 (incluso) e 10 (excluso), onde o expoente “n” sempre será um número pertencente ao conjunto dos números inteiros.
Notação Científica e Ordem de Grandeza
Ordem de grandeza
- Ninguém pode precisar o número de habitantes da China, que é o país mais populoso do mundo;
- Ninguém pode precisar o número de metros entre a terra e o sol;
- Ninguém pode precisar com exatidão a velocidade de translação e de rotação da terra;
- Ninguém pode precisar o tamanho da Via Láctea;
Mas em todos os casos citados acima podemos fazer uma boa estimativa, com maior ou menor precisão!
Então a Ordem de Grandeza foi criada para nos dar uma ideia aproximada de um valor que não temos como calcular com exatidão!
Por definição, “Ordem de Grandeza” é a potência de 10 mais próxima deste número.
Exemplos
Vamos chamar ordem de grandeza de OG!
A OG do número “23” é 101, pois 23 está mais próximo de 101 do que 102.
A OG do número “78” é 102, pois 78 está mais próximo de 102 do que 101.
A OG do número “3” é 100, pois 3 está mais próximo de 100 do que 101.
A ordem de grandeza do número “2” é 100, porque 2 está mais próximo de 100 do que 101.
Como calcular a Ordem de Grandeza
Para calcularmos a ordem de grandeza de um número, é preciso seguir algumas regras:
- Devemos escrever esse número em notação científica, no formato N = y⋅10n
- Verificar e comparar o valor de y com √10
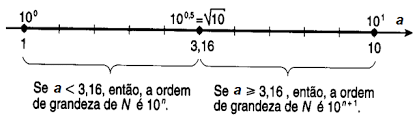
- Se y for menor do que √10 = 3,16 a OG do número será: 10n
- Se y for maior do que √10 = 3,16 a OG do número será: 10n+1
O valor √10 = 101/2 é o meio do caminho entre 100 e 101 , veja abaixo.
Exemplos:
Veja como calcular a Ordem de grandeza dos números abaixo:
- A OG do número 2,49⋅107 é 107 pois 2,49 < 3,16. Nesse caso é só manter o valor da base 10
- A OG do número 4,72⋅107 é 108 pois 4,72 > 3,16. Nesse caso é preciso somar uma unidade ao expoente da base 10
Notação Científica e Ordem de Grandeza
Para você entender melhor, veja abaixo uma aula sobre notação científica e ordem de Grandeza:
Exercícios Notação Científica e Ordem de Grandeza
(UFF-RJ) A luz proveniente do Sol demora, aproximadamente, 8 minutos para chegar à Terra.
A ordem de grandeza da distancia entre estes dois astros celestes, em km, é:
a) 103
b) 106
c) 108
d) 1010
e) 1023
Veja nesses link aulas top para você revisar antes da prova do Enem:
Resolução
Sabendo-se que a velocidade da luz é V = 3.108 m/s
e cada minuto tem 60 s, podemos transformar 8 min em s
8.60 = 480 s
1 s ———— 3.108 m
480 s ———— x
x = 3.108. 480 = 1440.108 = 1,44×103.108 = 1,44.1011 m = 1,44.108 km
x = 108 km.
Resposta C
(CEFET-SP) Uma pessoa percebeu que, durante 10 anos, para acender o seu aquecedor, consumiu uma caixa de palitos de fósforo a cada mês. Cada caixa apresenta, em média, 40 palitos.
A ordem de grandeza do número de palitos consumidos ao final dos 10 anos é:
a) 10
b) 102
c) 103
d) 104
e) 105
Resolução
Nesse caso temos 10 anos. Cada ano com 12meses . Gerando um total de 120 meses
Cada caixa tem 40 palitos, dando um total de 120 x 40 = 4.800 palitos.
Passando o valor 4.800 para notação científica temos 4.800 = 4,8.103
4,8 > 3,162 logo a ordem de grandeza do número 4,8.103 é 104.
Resposta D
(ENEM) A cor de uma estrela tem relação com a temperatura em sua superfície.
Estrelas não muito quentes (cerca de 3000 K) nos parecem avermelhadas. Já as estrelas amarelas, como o Sol, possuem temperatura em torno dos 6000K; as mais quentes são brancas ou azuis porque sua temperatura fica acima dos 10000 K.
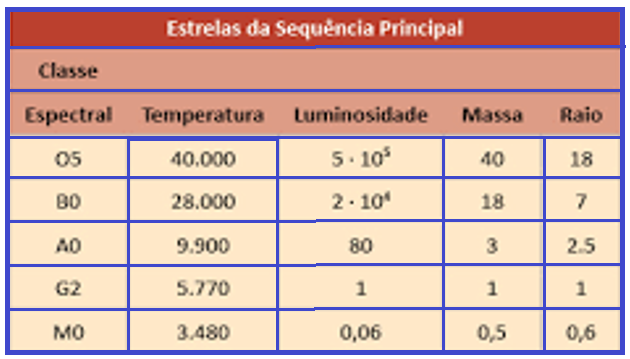
A tabela apresenta uma classificação espectral e outros dados para as estrelas dessas classes.
Se tomarmos uma estrela que tenha temperatura 5 vezes maior que a temperatura do Sol, qual será a ordem de grandeza de sua luminosidade?
A- 20 000 vezes a luminosidade do Sol.
B- 28 000 vezes a luminosidade do Sol.
C- 28 850 vezes a luminosidade do Sol.
D- 30 000 vezes a luminosidade do Sol.
E- 50 000 vezes a luminosidade do Sol.
Resolução
Temos que Te = temperatura da estrela e Ts = temperatura do sol
Te = 5.Ts = 5×5770 = 28850
Usando a tabela a temperatura de 28.850 pertence a classe espectral BO e sua luminosidade é equivalente a 2.104 =20000. Resposta A