Médias Aritméticas Simples e Ponderada [VIDEOAULA]

Podemos dizer que a medida mais usada de  tendência central são a Médias Aritméticas Simples e Ponderada.

Médias Aritméticas Simples e Ponderada

O número encontrado por essas médias, definirá um valor que representa todos os dados de uma sequência ou de uma tabela. Esse dado será o representante oficial dos demais.

Temos outros tipos de medidas como por exemplo: mediana a média Harmônica, desvio padrão e moda. Essas medidas são bem conhecidas pela Estatística, assunto bem recorrente em provas de Enem e concursos públicos.

Médias Aritméticas Simples e Ponderada

O que são as médias aritméticas simples e ponderada  ?

Média Aritmética Simples

A média aritmética simples é calculada através do somatório de todos os dados de uma determinada amostra, dividido pelo número de dados contidos nessa amostra

Para calcular a média aritmética simples usamos a fórmula:

 Fórmula

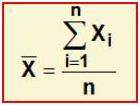
Onde:

• X =representa o valor calculado da média aritmética simples;
• Σ = símbolo do alfabeto grego (Sigma) que indica soma de todos os termos;
• n =número de elementos contidos na sequência, série, tabela, amostra ou população;
• i = 1 =>representa o primeiro elemento desta amostra;
• Xi =representa todos os valores da série

Exemplos de Médias Aritméticas Simples e Ponderada :

 Exercício 1 – Média Aritmética Simples:

Qual é a média de idade de um grupo de pessoas que tem 17, 30, 22, 15 e 45 anos?

Temos aqui uma amostra ou série de 5 idades diferentes. Isso significa que possuímos 5 termos, logo n=5

Resolução

Usando a fórmula de média aritmética simples temos:

X = (17 + 30 + 22 + 15 + 46)/5  =130 /5 => X = 26 anos

A média aritmética simples dessa amostragem foi de 26 anos

Exemplos de Médias Aritméticas Simples e Ponderada :

Exercício 2 – Média Aritmética Simples:

  Em uma escola, a média final, para obter a aprovação deverá se 7,0. João  tirou as seguintes notas em Português durante o ano letivo: 1º Bimestre 4,0, 2º Bimestre 6,5 , 3º Bimestre ,9,5 e 4º Bimestre 8,0!

Será que João conseguiu aprovação?

Resolução

X = (4 + 6,5 + 9,5  + 8)/4  =28 /5 => X = 7   Logo João foi aprovado

Média Aritmética Simples e  Ponderada.

———————————————————————–

O SEU CURSO ONLINE PARA O ENEM

 Faça a Diferença, Seja um Gênio Você Também!

———————————————————————–

Média Aritmética Ponderada

É usada para cálculos de média, onde os valores dos dados de uma determinada amostra  apresentam pesos relativos para cada um dos elementos

Vejamos a fórmula utilizada pela média ponderada:

A média aritmética ponderada _p de um conjunto de números x₁, x₂, x₃, …, x_n cuja importância relativa (“peso”) é respectivamente p₁, p₂, p₃, …, p_n é calculada da seguinte maneira:

Onde:

• Xp =Média ponderada
• n = número de elementos da amostra, série ou população;
• Xi =valor de cada elemento
• i = 1 = >início da soma pelo primeiro elemento;
• ∑ =Símbolo que indica somatório
• fi =pesos que serão utilizados e aplicado a cada dado

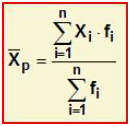
   Fórmula

Exemplos de Médias Aritméticas Simples e Ponderada :

Exercício 1 – Média Aritmética Ponderada

Como exemplo podemos imaginar as notas de uma determinada escola que considera cada bimestre com pesos diferentes. Digamos que  o peso dos bimestres vão aumentando e tem valores 1, 2, 3 e 4 respectivamente.

  Qual seria a nota de João (exemplo anterior) que obteve em Português durante o ano letivo: 1º Bimestre 4,0, 2º Bimestre 6,5 , 3º Bimestre ,9,5 e 4º Bimestre 8,0.

Resolução

Temos então:

1º Bimestre: nota 4,0 e peso 1
2º Bimestre: nota 6,5 e peso 2
3º Bimestre: nota 9,5 e peso 3
4º Bimestre: nota 8 e peso 4

Mp = (4 x 1 +6,5 x 2 + 9,5 x 3 + 8 x 4 )/(1 + 2+ 3 + 4)  =

Mp = (4 + 13 + 28,5 + 32) / 10  =

Mp = 77,5 / 10

Mp = 7,75