Matemática Financeira no Enem
A Matemática Financeira no Enem é cobrada de forma semelhante nas provas dos vestibulares e concursos. Esse assunto é recorrente e apresenta todo ano muitas questões nessa prova. Os assuntos relacionados a Matemática Financeira são: porcentagem, acréscimo, desconto, operação de compra e venda, lucro, prejuízo, juros simples e juros compostos. Abaixo segue uma lista de questões comentadas e outra lista com gabarito para você aprender, treinar e melhorar o seu desempenho.
Matemática Financeira no Enem
Porcentagem
PORCENTAGEM é a divisão por 100.
Como calcular porcentagem sem regra de 3 – cálculo rápido:
Trocar o “%” pela divisão por 100 e trocar o “de” por vezes (X)
Exemplo calcular 10% de 300 = (10/100) x 300 = 30
(lista de Exercícios): PORCENTAGEM, ACRÉSCIMOS E DESCONTOS
Acréscimo
Pf = Preço final e Pi = Preço inicial
tabela com taxa de acréscimo
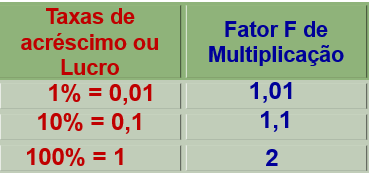
Pf = Pi x F
Fator F = 1 + TAXA
Exercício 1
Uma mercadoria que custava R$ 450,00 reais sofreu um reajuste de 15% de acordo com a inflação do período. Qual é o seu preço atual?
F = 1 + TAXA Pf = Pi x F
F = 1 + 0,15 = 1,15 Pf = 450 x 1,15 = R$ 517,50
Matemática Financeira no Enem
Desconto
Fator F = 1 – TAXA Pf = Pi x F
Tabela – taxas de descontos
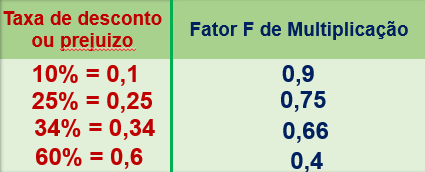
Exercício 2
Uma loja dá um desconto de 20 % nas compras à vista. Qual o valor de um computador de R$ 2.800,00 na promoção oferecida?
Resposta:
Pf = Pi x F F = 1 – 0,2 = 0,8
Pf = 2800 x 0,8 = 2.240,00
Lucro
Ao comprar uma mercadoria por R$100,00 e vendê-la por R$120,00, obtemos um lucro de R$20,00.
Prejuízo
Ao comprar uma mercadoria por R$100,00 e vendê-la por R$80,00, obtemos um prejuízo de R$20,00.
Matemática Financeira no Enem
OPERAÇÃO DE COMPRA E VENDA
Nessa operação temos 3 elementos fundamentais:
1) Quem vende (lojista) – Esse é o único que terá lucro ou prejuízo
2) Quem compra e o produtos – Ele paga o preço de venda que chamamos de Pv
3) Fabricante ou produtor – esse vende para o lojista e o mesmo paga o preço de compra que chamamos de Pc
Lucro
No lucro sempre o preço de venda é maior que o preço de compra: Pv > Pc
Pv = Preço de Venda Pc = Preço de Custo (compra)
O lucro é calculado por = Pv – Pc
Fórmula para calcular a operação de lucro: Pv = Pc + L
Exercício 3
Um produto custa R$ 100,00. Determine o valor da venda se o lucro de 20% incide sobre:
a) o custo
Resposta:
Pc = 100 Pv = ? L = 20% sobre o custo
L = 0,2 x Pc >>>> L = 0,2 x 100 = 20
Pv = Pc + L >>>> Pv = 100 + 20 = R$ 120
b) a venda
Resposta:
Pc = 100 Pv = ? L = 20% sobre a venda L = 0,2 x Pv
Pv = Pc + L >>>> Pv = 100 + 0,2.Pv >>>> Pv – 0,2.Pv = 100 >>>>
0,8.Pv = 100 >>>> Pv = 100/0,8 >>>> Pv = R$ 125
Aprenda Matemática de forma simples e em pouco tempo
Curso Gênio da Matemática >>> Método Inovador
Exercício 4
Vendi um objeto por R$ 600,00 lucrando 20% sobre o custo. Quanto custou o objeto?
Resposta:
Pv = R$ 600,00 >>>> L = 20% sobre o custo >>>> L = 0,20 x Pc
Pv = Pc + L
600 = Pc + 0,2.Pc >>>> 600 = 1,2.Pc >>>> 600/1,2 = Pc >>>> Pv = R$ 500
Matemática Financeira no Enem
Prejuízo
No prejuízo sempre o preço de venda é menor que o preço de compra: Pc > Pv
Temos 2 tipos de Prejuízos: Prejuízo sobre o custo e 07 . PORCENTAGEM, ACRÉSCIMOS E DESCONTOS 2
Prejuízo = Pc – Pv
Fórmula para calcular o prejuízo: Pv = Pc – P
Exercício 5
Uma pessoa vendeu certa mercadoria por R$ 600,00, tendo um prejuízo de 20% sobre o preço de venda. Determinar o preço de custo dessa mercadoria.
Resposta:
Pv = R$ 600,00 P = 20% sobre o venda >>>> P = 0,20 x Pv >>>> P = 0,2 x 600 = 120
Pc = ? >>>> Pv = Pc – P 600 = Pc – 120 >>>> 600+120 = Pc >>>> Pc = R$ 720
Matemática Financeira no Enem
Juros simples
Os juros simples representa o acréscimo que é somado ao capital inicial no final da aplicação.
O capital é o valor investido em uma aplicação financeira.
fórmula dos juros simples j = C. i.t
Sendo :
j = juros, C = capital, i = taxa, t= tempo.
Exercício
João aplica R$ 2.000, a juros simples, pelo prazo de 3 meses, com uma taxa de 3% ao mês. Quanto será pago de juros para João?
Resolução
J = C.i.t
J = 2.000 x 3 x 0,03 >>>> R$ 180. (valor pago de juros)
Matemática Financeira no Enem
Juros compostos
Os juros compostos são os acréscimos embutidos ao capital, ao fim de cada período de aplicação, no término de cada mês temos um novo capital, e isso é o que difere do juros simples.
Os bancos utilizam os juros compostos nas suas aplicações financeiras como poupanças e fundos.
A fórmula
M = C. (1 + i)t, em que:
M = montante, C = capital, i = taxa, t = tempo
Exercício 6
Usando o mesmo problema anterior:
João aplica R$ 2.000, a juros simples, pelo prazo de 3 meses, com uma taxa de 3% ao mês. Quanto será pago de juros para João?
C = R$ 2.000,00, t = 3 meses taxa (i) = 0, 03 (3% ao mês)
M = C. (1 + i)t >>>> M = 2.000 . (1 + 0, 03)3 >>>> M = 2.000 . 1,033 >>>> M = R$ 2.185,45
R$ 185,45 de juros ao final do empréstimo.
Exercício 7
Uma ação aumentou 10% em Janeiro e 20% em fevereiro, tendo uma queda de 5% em março. Qual é o aumento acumulado desses três meses?
M = C. 1,1.1,2.0,95 >>>> M = C. 1,254
1,254 = 1 + 0,254 (1 = 100% + 0,254 = 25,4%)
O aumento acumulado é de 25,4%
Exercício 8
(ENEM) São apresentadas três possibilidades de investimento para uma pessoa, com rentabilidades líquidas garantidas pelo período de um ano, conforme descritas: Investimento A: 3% ao mês; Investimento B: 36% ao ano; Investimento C: 18% ao semestre. As rentabilidades, para esses investimentos, incidem sobre o valor do período anterior.
O quadro fornece algumas aproximações.
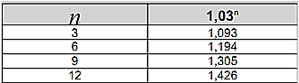Qual é o melhor investimento A, B ou C?
Resposta:
Investimento A:
3% ao mês >>>> 1 ano = 12 meses;
M = C.(1+i)t
M = C.(1+0,03)12 >>>> M = C.1,426 (temos uma rentabilidade de 42,6% no investimento A).
Investimento B:
36% ao ano >>>> M = C.1,36 (temos uma rentabilidade de 36,0% no investimento B).
Investimento C:
18% ao semestre >>>> 1 ano = 2 semestres;
M = C.(1+i)t >>>> M = C.(1 + 0,18)2 >>>> M = C.1,182
>>>> M = C.1,3924 (temos uma rentabilidade de 36,0% no investimento C).
