Juros Compostos como calcular – Matemática Financeira

juros Compostos como calcular

 Como falamos no post anterior:  “ Juros simples como calcular”   , o juro composto é aquele usado pelas instituições bancárias, nas aplicações financeiras da “famosa” caderneta de poupança, fundos e afins. O objetivo desse post é mostrar como calcular juros compostos.

O curso Gênio da Matemática tem um capítulo inteiro de Juros compostos para você aprofundar esse e os demais assuntos da Matemática. Confira o cursos de matemática mais completo do Brasil!

Dizemos que os juros compostos são os juros sobre juros. Isso significa que há maior rentabilidade quando comparados ao juro simples, já que o capital que incide a taxa muda todo o mês.

Então, os juros compostos, a cada período (t) de aplicação, que normalmente são os “meses” , é acrescido um valor de juros (J) que será proporcional ao valor do mês anterior, ou seja, a taxa de juros incidirá sobre o valor acumulado, que aumenta a cada período. Resumindo, o valor dos juros somado a cada período é sempre crescente.

Juro Composto

Vamos dar um exemplo: Numa aplicação financeira, em um fundo de investimentos, aplicamos R$ 5.000 a uma taxa de rendimento de 10% ao mês, após 3 meses teríamos um montante (M) de:

Resolvendo essa questão sem o uso da fórmula temos o seguinte cálculo:

M = 5.000 x 1,1 x 1,1 x 1,1

M= R$ 6.655,00

As taxas de Juros (i) são calculadas da seguinte maneira:

Nomenclatura de taxas – Como calcular juros Compostos

    20% a.m.   vinte por cento ao mês

     5%  a.d.     Cinco por cento ao dia

     30% a.a.     trinta por cento ao ano

     7%  a.s. Sete por cento ao semestre

     70% a.t. setenta por cento ao trimestre

Como contar o prazo do: Juro Exato e Juro Comercial 

Juro exato e juro comercial referem-se a contagem de tempo, exemplo 

Juro Comercial:    Ano = 360 dias e o     Mês = 30 dias

Juro Exato:      Ano = 365 ou 366 dias (ano bissexto)   e o    Mês = Segue o Calendário   Ex.:       Fevereiro = 28 ou 29 dias ou Janeiro = 31 dias

Juros Compostos como calcular

fórmula de juros compostos

M = C + J

fórmula de juros compostos

J = juros P = principal (capital) i = taxa de juros t = número de períodos (tempo

Como calcular juros Compostos 
Para o cálculo de juros compostos é necessário o
 uso de uma calculadora financeira, científica ou até mesmo o uso de uma tabela. 
Essa tabela normalmente é dada nas provas de concursos públicos, já que não é
 permitido o uso de calculadoras na prova.

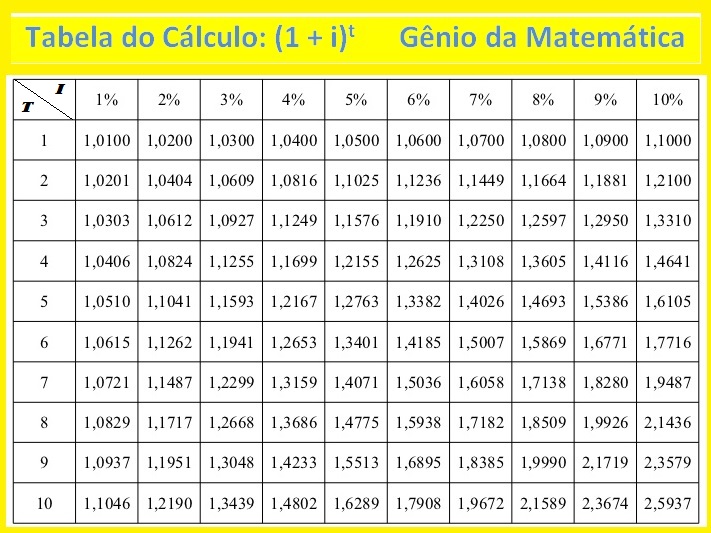
Juros compostos matemática financeira

 Exemplo 1

    Vamos agora resolver a questão anterior, só que com o uso e ajuda da fórmula e fornecendo a tabela de juros compostos. 

a) No caso anterior tínhamos aplicados R$ 5.000 a uma taxa de rendimento de 10% ao mês, após 3 meses teríamos um montante (M) de:

Resolução:  como calcular juros compostos

M = ?
C = capital inicial = 5.000,00
i = taxa de juros = 10% am
t = tempo = 3 meses

Vamos agora localizar na quarta linha da última coluna, onde t=3 e i=10%, o valor de (1 + i)^t = 1,331

substituindo na fórmula de juros compostos:  

                                             M = C .  (1 + i)^t

                                             M = 5.000 . (1 + 0,1)³

                                             M = 5.000 . 1,331

                                             M = 6,655

 Exemplo 2

b) Um mutuário comprou um apartamento por R$ 100.000,00 financiado por um banco com taxa de juros de 15% ao ano, financiado em 10 anos. Logo no primeiro mês, ele perde o emprego e não consegue pagar nenhuma prestação. Qual será o valor do montante (tudo que ele deve) ao final de 10 anos?

Resolução:  como calcular juros compostos

M = montante
C = capital inicial = 100.000,00
i = taxa de juros = 15% ao ano
t = tempo = 10 anos

Nesse caso a tabela não fornece o valor (1 + i)^t  pois temos aqui i = 15% e a tabela vai até 10%, então precisamos recorrer a uma calculadora o valor de (1 + 0,15)¹⁰ = (1,15)¹⁰= 40,455577

substituindo na fórmula de juros compostos:

  M = C .  (1 + i)^t

M = 10.000 (1+ 0,15)¹⁰

M = 404.555,77

 Exemplo 3

c) O montante de R$ 17.408,94 foi obtido após a aplicação de um capital a juro composto por um período de 6 meses à taxa de 1% a.m. Qual foi o capital aplicado?

Resolução:  como calcular juros compostos

C = ?

M = 17.408,94

i =1 % a.m. = 0,01 a.m.

t = 6 meses

substituindo na fórmula de juros compostos:   M = C .  (1 + i)^t

                                             17.408,94 = C .  (1 + 0,01)⁶

Vamos agora localizar na sétima linha da segunda coluna, onde t=6 e i=1%, o valor de (1 + i)^t = 1,0615

17.408,94 = C .  1,0615

C = 17.408,94 / 1,0615

C = 16.400,00

Exemplo 4

d) Qual o tempo que devemos aplicar um capital de R$ 800,00 a uma taxa de juros de 3% ao mês, para que gere um montante de R$ 1.444,89?   Dados log,013 = 0,0128 e log1,806=0,2567

Resolução:   como calcular juros compostos

C = R$ 800,00

M = R$ 1.444,89

i =3 % a.m. = 0,03 a.m.

t = ?

           substituindo na fórmula de juros compostos

                        M = C .  (1 + i)^t

                    1.444,89 = 800 .  (1 + 0,03)^t

                   1.444,89 / 800 =  (1 + 0,03)^t

                   1,806 =  (1 + 0,03)^t

Par resolver essa equação exponencial,  precisamos de uma calculadora científica ou, até mesmo, dos dados de logaritmos fornecidos na questão.

 (1 + 0,03)^t = 1,806  aplicando logaritmo nos dois lados da equação exponencial temos:

log (1,03)^t = log 1,806   aplicando a propriedade do expoente  dos logaritmos temos

t . log 1,03 = log 1,806   usando os dados fornecidos log,013 = 0,128 e log1,806=0,2567  

t . 0,0128 = 0,2567

t = 20 meses

Confira nosso vídeo no youtube que fala sobre Matemática Financeira e muito mais. Clique aqui!

Acredito que esse assunto deveria ser aprendido por todas as pessoas e não só por vestibulando e concurseiros.

Se você vai comprar uma roupa, um carro ou  até mesmo uma casa saiba que nessas operações de compra e venda estão embutidos os juros compostos e você pode, nessa compra à prazo, estar levando uma e pagando duas ou até mesmo quatro vezes o valor do produto comprado.

Um exemplo clássico é a simples compra de um carro à prazo. Procure escolher um banco com taxas menores e não aqueles que o vendedor mostra pra você na hora da compra. Normalmente o que é mostrado são os bancos que lucram com maiores taxas e sua prestação poderá aumentar um valor considerável de banco para banco.

Se você quer aprofundar esse ou outros assuntos clique no banner abaixo e conheça a melhor plataforma de ensino de Matemática do Brasil. Saiba mais clicando aqui!