Veja aqui tudo sobre módulo, função modular e equação modular

Função Modular e Equação Modular

Módulo de um número real

O módulo representa sempre o tamanho de um número real ou de uma função. O módulo de um número x  também é representado por: |x|

Podemos dizer então que o módulo de um número real, representado por |x| será  o seu valor absoluto, ou seja:

|x| = x, se x≥0  ou |x|= x, se x>0

|x| = −x, se x≤0 ou |x| = −x, se x<0

” Função Modular e Equação Modular “

Propriedades envolvendo Módulo  

Propriedades  Modulares de um Número Real

• |x| = |-x| com x ∊ R;
• |x²| = |x|² = x² com x ∊ R;
• |x . y| = |x| . |y|, com x e y ∊ R;
• |x + y| ≤ |x| + |y|, com x e y ∊ R

a) Qual é o módulo de 3?

Para responder precisamos interpretar o significado:

Qual é o tamanho do número 3? A resposta é 3 mesmo

b) Qual é o módulo  de |-3|?

Agora qual é o tamanho do número -3? A resposta também será 3

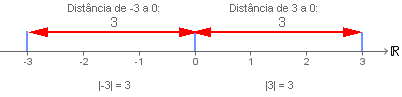
Ou seja , |3| = 3   e |-3|= 3

Veja a representação gráfica abaixo e compare como o tamanho de ambos é o mesmo!

Função Modular e Equação Modular

Exercícios de módulo de um número real

a)  2.| 5| =

b) | -7 | + | -2 | =

c) | -3 | – | +8 | =

d) | -5 + 3 | = 

e) | -5 | + | +3  | =

f) | 2 – √5 | =

g) | √5 – 2 | =

h) | 5 – 8√2 | =

Respostas

a) 10        b) 9       c) -5   d) 2        e)  8       f) – 2 + √5         g) √5 – 2         h) – 5 + 8√2

O mesmo podemos demostrar com as funções modulares!

Função Modular e Equação Modular

Definição de Funções Modulares

Dado um número real x, sempre existe  |x| e seu valor é único.

Definimos função modular, sendo f: R → R  por:   f(x) = |x| ou y = |x|

Seguindo os mesmos princípios dos números reais, o módulo de uma função representará o tamanho dessa função, logo:

f(x) = x, se x≥ 0
ou
f(x) = – x, se x < 0

Para entender melhor a função modular, vamos entender seus gráficos!

Gráfico de função Modular

O gráfico da função modular muda a posição para positivo na intersecção com o eixo x.

Abaixo do eixo x  teremos valores negativos e na representação gráfica da função modular os valores negativos ficam positivos, veja abaixo!

Exemplos:

f(x) = x

f(x) = |x|

f(x) = x² + 2x – 3

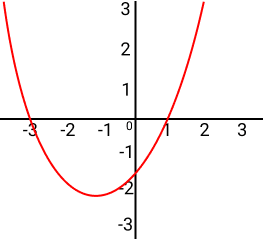
f(x) = |x² + 2x – 3|

Função Modular e Equação Modular

Equações Modulares

Equações modulares são aquelas em que a incógnita aparece dentro de módulos.

Para resolvê-las é útil relembrar as propriedades envolvendo módulos vistas no início desse post!

Exemplo 1

|x + 3| = 6
Condições:
x + 3 = 6 ou x + 3 = – 6
Solução:
x + 3 = 6 → x = 6 – 3 → x = 3
x + 3 = –6 → x = – 6 – 3 → x = – 9

S = {3; -9}

Exemplo 2

|2x – 6| = x + 2
Condições:

x + 2 ≥ 0  ou seja  x ≥ -2
2x – 6 = x + 2    ou    2x – 6 = – (x + 2)

Resolução:
2x – 6 = x + 2→ 2x – x = 6 + 2 → x = 8

2x – 6 = – (x + 2)→ 2x – 6 = – x – 2 → 2x + x = –2 + 6 → 3x = 4    →  x = 4/3

os valores encontrados , satisfazem a condição  x ≥ -2, logo o conjunto solução é {4/3 ;  8}

Exemplo 3

|2x – 1| = |-x + 5|

2x – 1 = – x + 5     →    2x + x = 1  + 5    →     3x = 6     →    x = 2 

2x – 1 = – (- x + 5)   →     2x + 1 = + x – 5     →   2x – x = – 5 – 1     →      x = -6 (Impossível)

Resposta: {2}

Exemplo 4

|x² – x – 4| = 2

x² – x – 4 = 2      →       x² – x –  4 – 2 = 0     →       x² – x –  6 = 0

Resolvendo a equação do segundo grau por Bhaskara ou soma e produto chegamos a duas raízes reais:    x’ = -2 e x” = 3

Veja aqui como resolver equação do 2⁰ grau por soma e produto: LINK 

x² – x – 4 = – 2 → x² – x – 4 + 2 = 0 → x² – x – 2= 0

Resolvendo a equação do segundo grau por Bhaskara ou soma e produto chegamos a duas raízes reais:  x’ = 2   e   x” =-1

S = {-2, -1, 2, 3}

Exercícios Equações Modulares (questões difíceis!)

01) (UFV) Se x e y são números reais quaisquer, então é CORRETO afirmar que:

a) se x² < y², então x < y.

b) se x < y, então x² < y².

c) se x² – y² = 0, então |x| = |y|.

d) √(x² + y²) = x + y.

e) – x < 0.

02. (UEM) Considerando o conjunto A = {x ∈ R; – 3≤ x ≤ 3}, assinale a(s) alternativa(s) correta(s). 01) O conjunto das soluções da inequação x² < 9 é igual ao conjunto A.

02) O conjunto A contém o conjunto das soluções da inequação – 5x² – 14x + 3≥ 0.

04) A reunião dos conjuntos das soluções das equações (5x – 8)² = – 21 e |5x – 3| = – 8 está contida em A.

08) O conjunto-solução da equação |2x – 5| = |8x + 3| está contido no conjunto A.

16) O menor elemento do conjunto A pertence à interseção dos conjuntos das soluções das inequações x≤ 9   e   x² – 7x + 10≤ 0.

32) A interseção entre o conjunto A e o conjunto das soluções da inequação x² – 7x + 10 ≤ 0 é o conjunto B = {x ∈ R; 2≤ x < 3}.

03) (U. Tuiuti – PR)

As raízes reais da equação |xl ² + |x| – 6 = 0 são tais que:

a) a soma delas é – 1.

b) o produto delas é – 6.

c) ambas são positivas.

d) o produto delas é – 4.

e) n.d.a.

4) (U.F. Juiz de Fora-MG)

O número de soluções negativas da equação | 5x-6 | = x² é:

a) 0

b) 1

c) 2

d) 3

e) 4

Respostas

1) c     

2) alternativas corretas: 02, 04, 08 e 16 alternativas incorretas: 01 e 32

3) Para resolver essa questão use y = | x | e considere só o valor positivo de y. As raízes são -2 e 2 e a resposta é D

4) Obteremos 4 raízes com as duas equações do segundo grau: {1, 2, -6 e 49} logo só teremos uma raiz negativa e a resposta é B