Função Exponencial [Parte 1]
Função Exponencial
A função exponencial é uma função Matemática que apresenta um crescimento ou decrescimento acelerado.
Essa função aparece em inúmeras situações e em muitas áreas do conhecimento. Como exemplo podemos dizer que ela se apresenta em múltiplas situações nos cálculos das quatro ciências exatas, além de ser muito estudada no segundo grau, nas disciplinas de Física, Química, Matemática e Biologia.
Ela também aparece em outras áreas como: Economia, Engenharia, Astronomia, Geografia, Medicina etc…
Leia também:
Quer aprender um pouco mais sobre Trigonometria?
Na Química por exemplo, a função exponencial aparece no capítulo de Radioatividade, nos gráficos de meia vida de átomos radioativos.
Esse tipo de exponencial é chamado de decaimento radioativo.
O carbono 14 tem meia vida igual a 5730 anos e esse termo é chamado de “meia vida”, devido ao fato de que a cada 5730 anos a massa de uma amostra desse material radioativo, sempre se reduzirá pela metade.
Aqui, no gráfico abaixo, temos o decaimento radioativo do carbono 14
Decaimento radioativo do carbono 14
Na Matemática, também estuda a função exponencial em diversos conteúdos. No caso, do gráfico em questão, podemos verificar a comparação dos juros simples, cuja função é Linear, com os Juros Compostos que apresenta uma função exponencial.
função exponencial dos juros simples X juros compostos
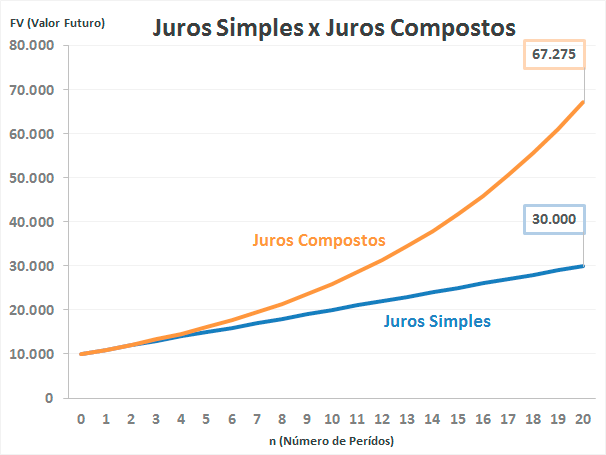
A Biologia também pode apresentar a função exponencial em diversas situações, e uma delas é envolvendo o crescimento de bactérias em uma determinada colônia.
Função exponencial com o número de bactérias
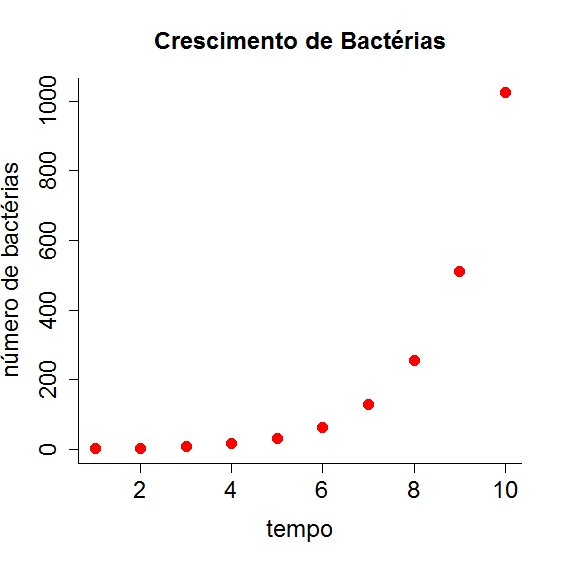
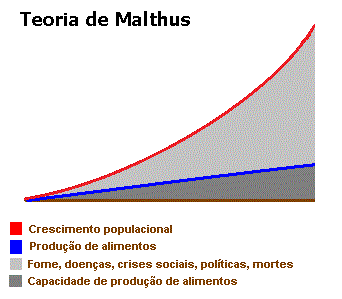
Na Geografia temos o famoso crescimento populacional, da teoria de Malthus.
“Malthus percebera que o crescimento populacional entre os anos 1785 e 1790 havia dobrado, em razão do aumento da produção de alimentos, das melhores condições sanitárias e do aperfeiçoamento no combate às doenças – benefícios decorrentes da revolução industrial. Essas melhorias fizeram com que a taxa de mortalidade diminuísse e a taxa de natalidade aumentasse.”
https://pt.wikipedia.org/wiki/Teoria_populacional_malthusiana
Função Exponencial de Malthus
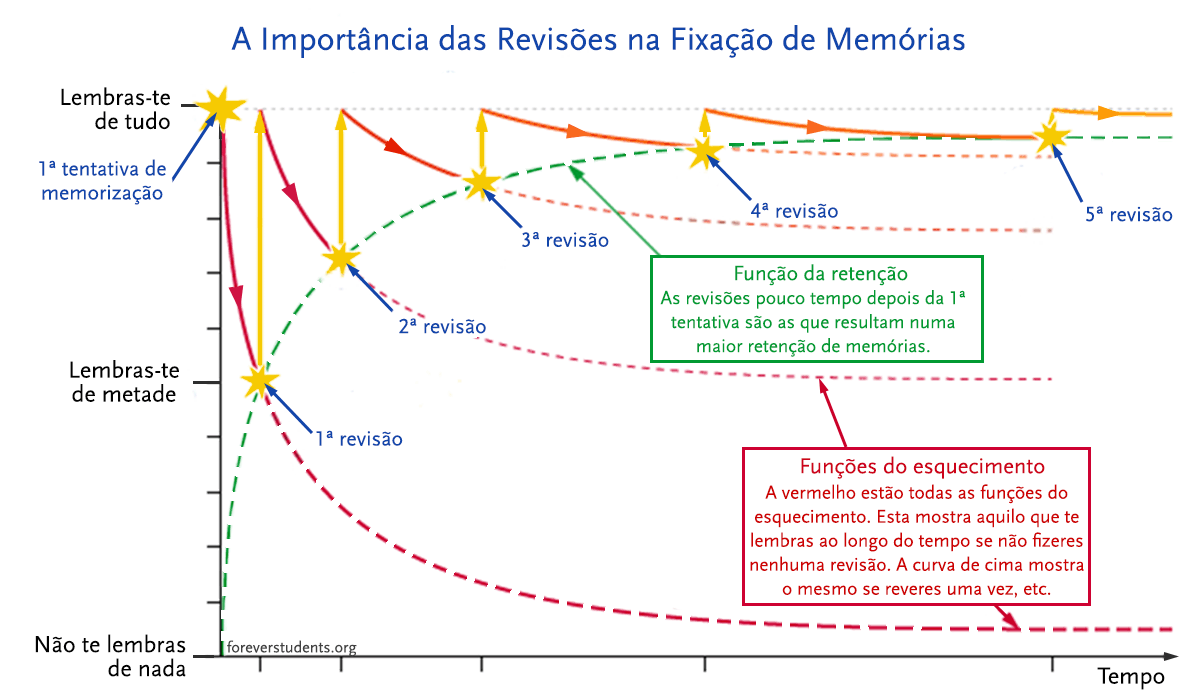
Atualmente muitos trabalhos de neurocientistas e educadores tem tido resultados extraordinários e o uso da função exponencial pode ser encontrado em suas pesquisas.
O gráfico de uma função exponencial permite o estudo de situações que se enquadram em uma curva de crescimento ou decrescimento, sendo possível analisar as quantidades relacionadas à curva, por isso os Psicólogos e Educadores utilizam-se da exponencial a fim de demonstrarem as curvas de aprendizagem.
Curva de esquecimento X número de revisões
Em razão de suas propriedades, a função exponencial é considerada uma importante ferramenta da Matemática e de todas as áreas do conhecimento, atuando em inúmeras situações cotidianas e ajudando de forma incisiva na obtenção de resultados que exigem análises quantitativa e qualitativa.
Podemos observar que a aplicabilidade da função exponencial é gigante e infinita. Veja do exemplo de seu uso na economia:
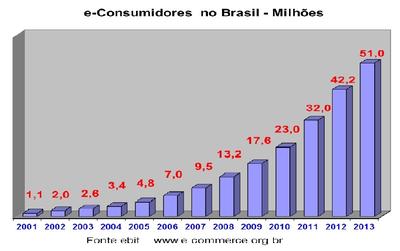
Abaixo temos um gráfico que mostra o comportamento do tipo de compra e dos valores investidos em e-commerce no Brasil.
Em 2001,poucos tinham o hábito de comprar pela internet. As pessoas além de não conhecer essa extraordinária opção, que facilita muito a vida de todos, havia uma desconfiança nesse tipo de comércio. Muitos acreditavam que comprar pela internet era inseguro e a compra poderia não ser entregue. Com o tempo essa mentalidade foi mudando e atualmente quase todo brasileiro com cartão de crédito, já fez essa operação. Os dados são criptografados e é quase impossível alguém burlar as regras.
Uma dica importante é fazer suas compras em um site que tenha segurança e isso é fácil de verificar. Na hora de passar o cartão em uma compra virtual, não insira seus dados em um site que não seja “https”. Se for “http” caia fora pois ele não terá nenhuma segurança.
Número de pessoas que compraram na internet
Enfim, eu coloquei aqui alguns exemplos da usabilidade da função exponencial, que normalmente é aprendida no primeiro ano do segundo Grau. O seu uso é ilimitado e está presente em todas as áreas do conhecimento. Os exemplos são muitos.
No próximo post eu mostrarei em uma vídeo aula, como construir um gráfico da função exponencial, com muita simplicidade, sem precisar ficar plotando pontos. Certamente você precisará dessa informação para resolver uma questão no colégio, Enem, vestibular ou até mesmo em algum concurso público que tenha em seu programa essa função.
Caso queira aprofundar os seus conhecimentos com a teoria e com muitos exercícios resolvidos em vídeo aulas desse conteúdo, acesse o nosso curso online Gênio da Matemática.
