Congruência e Semelhança de Figuras Planas

Nesse artigo iremos falar sobre um assunto muito recorrente em provas do Enem e vestibular, trataremos de congruência e semelhança de figuras planas . Teremos também vídeos para melhorar ainda mais o seu aprendizado, com teoria e correção dos exercícios aqui dispostos.

Pontos Notáveis de um Triângulo

Antes de discutirmos a congruência e semelhança de figuras planas, vamos relembrar alguns conceitos básicos:

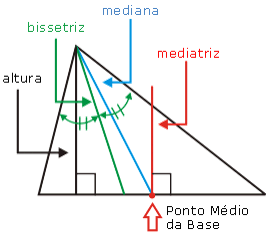
• Altura: segmento de reta que liga um vértice com a base de um triângulo com o vértice oposto formando um ângulo de 90⁰ com a mesma.
• Bissetriz: segmento de reta que liga um vértice com a base de um triângulo formando dois ângulos exatamente iguais ou congruentes no mesmo.
• Mediana: segmento de reta que liga  o vértice de um triângulo com o  ponto médio da base do mesmo.
• Mediatriz: segmento de reta ou reta formada, partindo do ponto médio da base de um triângulo com a formação de um ângulo de 90⁰ com o mesmo.

 Congruência e Semelhança de Figuras Planas

Congruência 

Duas figuras congruentes nem sempre são iguais.

Quando um triângulo tiver 3 ângulos iguais, dizemos que os ângulos são congruentes mas não podemos afirmar que o os triângulos são congruentes. Para que os triângulos sejam congruentes é preciso ter os 3 lados iguais. Nesse caso teremos as duas situações ângulos e lados congruentes.

Abaixo temos um quadrilátero congruente, já que todos os ângulos e todos os lados são iguais.

A igualdade entre eles deve ser obrigatoriamente entre as medidas de seus lados e de seus ângulos.

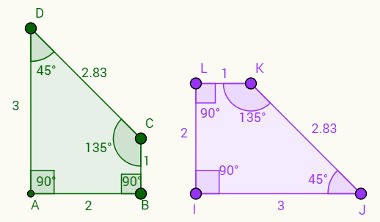
 Congruência e Semelhança de Figuras Planas

Semelhança de triângulos

Por exemplo, os triângulos abaixo são semelhantes, mas não congruentes:

O símbolo  significa “semelhante”. 

O simbolo ≡ significa congruência

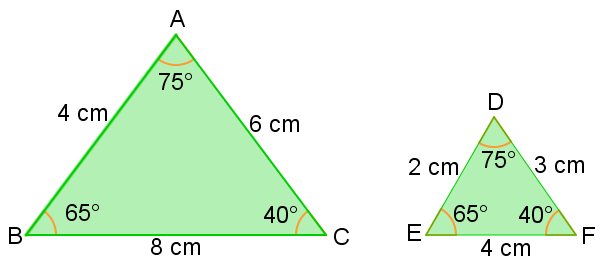
                                          Semelhança de triângulos   △ABC∼△DEF

No caso acima temos dois ângulos congruentes, ou seja,  iguais. Porém os lados, não são congruentes,  são chamados de homólogos. Então nesse caso há uma proporcionalidade entre os lados.

Outro dado importante é que o terceiro ângulo de ambos os triângulos é igual a 75⁰,

pois  65⁰ + 40⁰ + 75⁰ = 180⁰

Observe que as dimensões do triângulo maior correspondem ao dobro do menor

 AB/DE = BC/EF = AC/DF ⇒4/2 = 8/4 = 6/3 = 2

A razão de proporcionalidade é 2, ou seja, k = 2.

Congruência e Semelhança de Figuras Planas

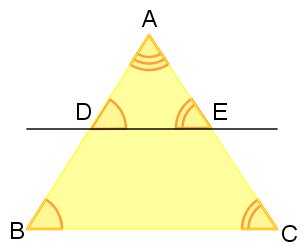
Teorema fundamental da semelhança

Havendo uma reta paralela a qualquer um dos lados do triângulo, com a mesma cortando os outros dois lados em pontos diferentes, haverá a formação de dois triângulos semelhantes.

Congruência e Semelhança de Figuras Planas

Casos de semelhança de triângulos

Primeiramente precisamos saber se os dois triângulos são semelhantes. A proporcionalidade poderá ser verificada através de alguns casos especiais, sem necessidade de conhecer todos os lados e/ou ângulos.

Congruência e Semelhança de Figuras Planas

1) Caso AA (ângulo, ângulo)

Dois triângulos serão semelhantes se, e somente se, 2  ângulos forem iguais (congruentes).

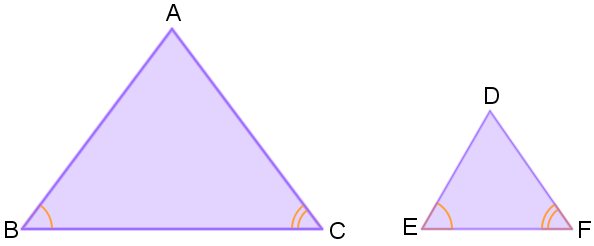
                                                                            Linguagem de semelhança: △ABC ∼ △DEF

Congruência e Semelhança de Figuras Planas

MATEMÁTICA PARA ENEM E VESTIBULAR

2) LAL (lado,ângulo, lado)

Observe que as medidas dos lados do triângulo maior é o dobro do menor (são proporcionais), e o ângulo formado entre eles é o mesmo.  logo existe semelhança!

Dois triângulos serão semelhantes se, e somente se, eles tiverem dois lados respectivamente proporcionais e se os ângulos formados por esses lados forem congruentes.

Congruência e Semelhança de Figuras Planas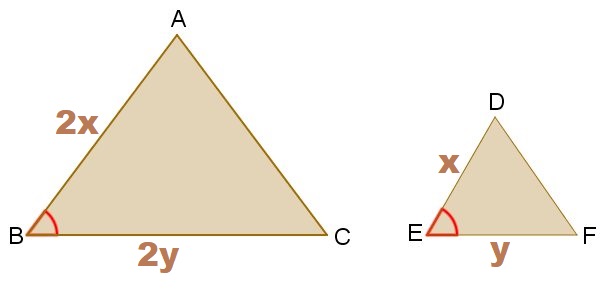

Congruência e Semelhança de Figuras Planas

3) LLL (lado, lado, lado)

Haverá semelhança se todos os lados de um triângulo forem proporcionais

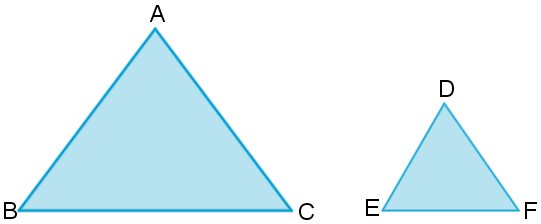
                                                                 AB/DE = BC/EF = AC/DF 

 Logo temos dois triângulos semelhantes ⟺△ABC∼△DEF

Exercícios

(ENEM) A rampa de um hospital tem na sua parte mais elevada uma altura de 2,2 metros. Um paciente ao caminhar sobre a rampa percebe que se deslocou 3,2 metros e alcançou uma altura de 0,8 metro.

A distância, em metros, que o paciente ainda deve caminhar para atingir o ponto mais alto da rampa é

A) 1,16 metros

B) 3,0 metros

C) 5,4 metros

D) 5,6 metros

E) 7,04 metros

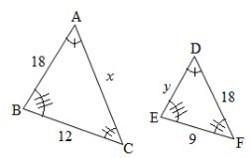
2) Qual o valor de x e y no triângulo DEF?

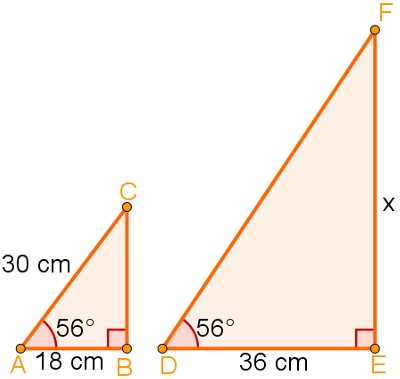
3) As figuras abaixo nos mostram pares de triângulos semelhantes, dessa forma calcule os valores de e x e y:

Respostas

1) D

2) x = 60 cm e y =48 cm

3) y=13,5  e  x=24