Gráfico da Função Exponencial [vídeo]

Gráfico da Função Exponencial
O gráfico da função exponencial é representado por uma curva que cresce ou decresce acentuadamente no plano cartesiano e ele pode ser construído numa fração de segundos usando uma simples técnica que é aplicada em todas as funções que são explicadas no curso Gênio da Matemática.
Todo tipo de função, na Matemática, apresenta duas variáveis e a função exponencial não poderá ser diferente.
As duas variáveis são: variável “x” que chamamos de independente e a varável “Y”que chamamos de variável dependente.
Na função exponencial a variável “x” está no expoente.
Leia também
Veja um exemplo:
y = 4 x
y = 5 x + 4
y = 0,8 x
y = 6 x
Teremos então uma lei que regerá essa função:
f: R→R tal que y = a x, sendo que a > 1 ou 0 < a < 1.
Na função exponencial temos que a base “a”, que será elevada ao expoente x sempre será maior que zero e diferente de 1!
A função exponencial será sempre representada por uma curva semelhante aos gráficos abaixo.
No gráfico da esquerda temos a > 1 e no da direita temos o valor de “a” no intervalo 0 < a < 1.
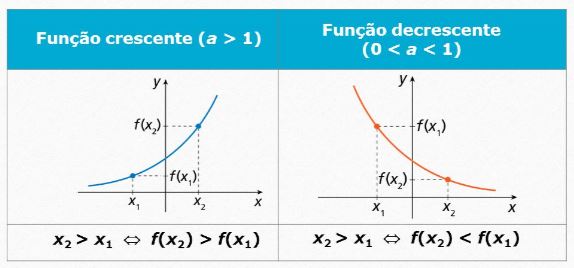
Gráfico da Função Exponencial crescente e decrescente
Gráfico 1 Gráfico 2
Dizemos que o gráfico da esquerda (1) representa uma função crescente pois a medida que o valor de “x” aumenta o de “Y” também aumenta.
O gráfico da direita (2) representa uma função decrescente pois a medida que o valor de “x” aumenta o de “Y” diminui.
Abaixo é mostrado uma forma, que não é muito prática, de construir um gráfico de uma função exponencial.
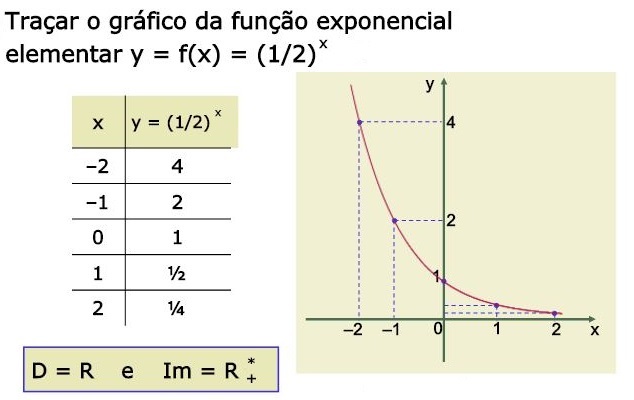
Gráfico da Função Exponencial Decrescente
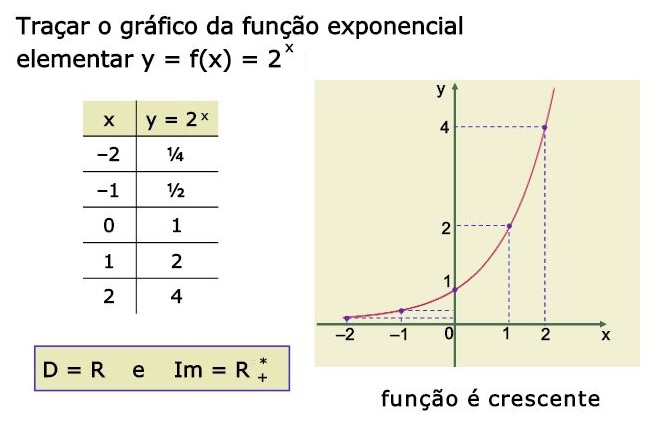
Gráfico da Função Exponencial Crescente
Plotar pontos, construindo uma tabela de valores aleatórios de x, substituindo na função, certamente não é a maneira mais adequada de se resolver uma questão envolvendo gráfico da função exponencial. A explicação é simples há técnicas muito efetivas e bem mais simples de se construir um gráfico dessa função sem muito trabalho.
Faça os exercícios a seguir e confira as resoluções que são apresentadas no vídeo abaixo
a) y = 5x
b) y = (1/3)x
c) y = (4/3)x
d) y = 7-x
e) f (x) = (5/16) -x
f) f (x) = (0,3)x
g) y = -2 . 3x
h) y = -2 (1/3)x
i) y = -3x
Assista ao vídeo abaixo e aprenda a construção de gráficos dessa função de uma maneira muito simples.
Caso queira aprofundar os seus conhecimentos com a teoria e com muitos exercícios resolvidos em vídeo aulas desse conteúdo, acesse o nosso curso online Gênio da Matemática.













