Ângulos da Circunferência [Vídeo]

Está na hora de aprender definitivamente como determinar todos os ângulos da circunferência . Esse capítulo pertence a Geometria Plana e é muito cobrado nos vestibulares, principalmente aqueles voltados para a área militar. Então vamos ao estudo sobre ângulos da circunferência !
Logo a seguir você encontrará uma vídeo aula com o resumo dos conteúdos e com todos os exercícios resolvidos abaixo.
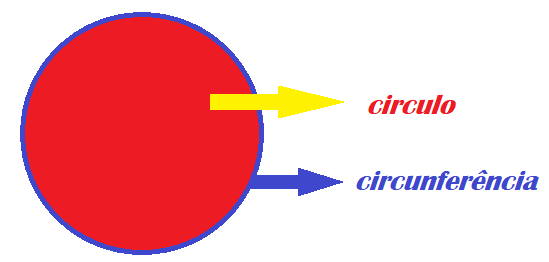
Antes vamos conhecer alguns conceitos. Você sabe qual é a diferença entre circunferência e círculo?
Bem, a circunferência é a linha que contorna toda a área do círculo. Veja no desenho a seguir:
Vamos lá!
Ângulos da Circunferência
Ângulos da Circunferência – Geometria Plana
Ângulos da Circunferência
Vamos agora ver quais são os principais ângulos que são formados na nossa circunferência!
1) Ângulo Central
Ângulo com vértice no centro da circunferência!
Propriedade:
O ângulo central apresenta a mesma medida do arco formado por seus lados, ou seja:
a medida do ângulo AÔB igual à medida do arco AB.
α = AB
Ângulos da Circunferência
2) Ângulo inscrito
Ângulo cujo vértice é um ponto da circunferência – Ângulo Inscrito.
Propriedade:
a medida do ângulo inscrito equivale à metade da medida do arco formado por seus lados, ou seja:
α = AB/2
Ângulos da Circunferência
3) Arco Capaz
Como a medida do ângulo inscrito é sempre a metade da medida do arco que ele estabelece na circunferência, qualquer arco formado pelos mesmos dois pontos terão o mesmo ângulo α.
Ângulos da Circunferência
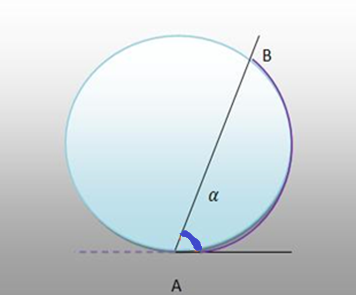
4) Ângulo de segmento
É todo ângulo em que o vértice pertence à circunferência, sendo um dos lados secante e o outro tangente. A medida do ângulo de segmento é a metade do arco por ele estabelecido.
Na figura abaixo, α é considerado um ângulo de segmento, que estabelece na circunferência o arco AB.
α = AB/2
Ângulos da Circunferência
5) Ângulo excêntrico exterior
Na figura, o ângulo APB é excêntrico exterior e determina na circunferência os arcos AB e CD.
A medida do ângulo APB é a metade da diferença entre os arcos AB e CD.
Propriedade:
o ângulo α equivale à metade da diferença entre as medidas dos arcos formados pelos seus lados, ou seja:
α = (AB – CD)/2
Ângulos da Circunferência
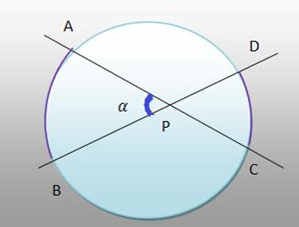
6) Ângulo excêntrico interior
Propriedade:
o ângulo excêntrico interno possui medida igual à metade da soma dos arcos formados pelos seus lados, ou seja:
A medida do ângulo APB é a metade da soma dos arcos AB e CD
Ângulo com vértice no interior da circunferência
Ângulo excêntrico interno.
α = (AB + CD)/2
Ângulos da Circunferência
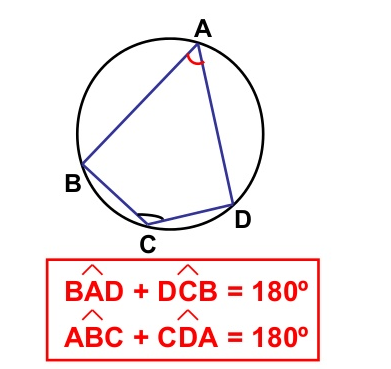
7) Quadrilátero Inscrito na Circunferência
Todo quadrilátero inscrito em uma circunferência apresenta ângulos opostos suplementares!
Exercícios (todos estão corrigidos e comentados na videoaula acima)!
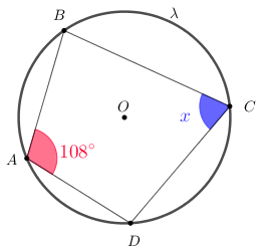
1) Qual o valor de x
2) Na figura, o ângulo ABC mede 760. Calcule a medida angular do arco ADC.
3) Na figura, A,B e C são pontos da circunferência λ de centro em O e a e c são as medidas dos ângulos com vértices em A e C, respectivamente.
Determine, em graus, a soma a + c.
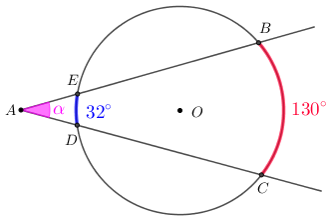
4) Na figura, o arco BC mede 1300 e DE mede 320. Qual o valor de α?
5) Determine a medida θ indicada na figura abaixo.
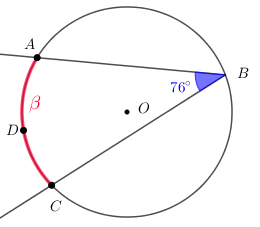
6) Determine a medida em graus β indicada na figura abaixo.