Prova de Matemática Comentada

 UFRGS 2016 – Prova Resolvida

Vídeos -Prova ENEM Comentada Matemática 2015 

Questão 26. Resposta (A)

Total = 912      Córnea = 487

487/ 912 = 0,53 → 53%

Questão 27. Resposta (C)

1992:        1 030 000 000__________________ 100%

2012:        842 000 000    _____________  x

x =81,74%

100%  – 81,74%   = Declínio de 18,26%

Questão 28. Resposta (B)

Em 2000  o tempo total foi de 6,5h = 6,6 x 60 = 390 min

390 x 0,9 x 0,9 = 315,9 min = 315,9 min =  5 x 60 + 16  = 5 h + 16 min

Prova de Matemática Comentada – UFRGS 2016 – Prova Resolvida

Questão 29. Resposta (B)

x + y = 13            x ∙ y = 1           e     x² + y² = ?

(x + y)² = 13²

x² + 2xy + y² = 169

x² + 2 ∙ 1  + y²  = 169

x² + y² = 1169 – 2 =167

Questão 30. Resposta(D)

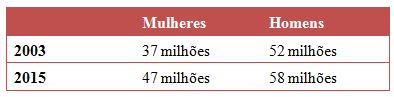
A população feminina economicamente ativa aumentou em        (47 – 37) / 37 = 27%

A população masculina economicamente ativa aumentou em   (58 – 52) / 52  =  11,5 %

Questão 31. Resposta (C) 

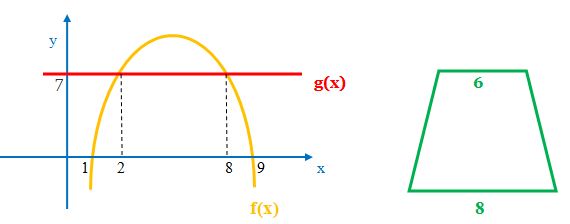
Área do Trapézio = (B + b) . h / 2 = (8 + 6).7 / 2 =  49

Questão 32. Resposta (D)

O primeiro termo tem  soma 1+0+1= 2

O Segundo termo tem soma 1+0+1+0+1+0+1 = 4

E assim sucessivamente com o terceiro termo dando soma = 6

Então queremos a soma da PA com vinte termos ou n=20.

PA: (2, 4, 6…)

a_n = a₁ + (n-1) . r          a_n = 2 + (20 -1) . 2 = 40

S = (a₁+ a_n).n/2          S = (2 + 40) . 20 / 2 = 420

Questão 33. Resposta (E)

s medidas são sempre proporcionais. Se a altura do segundo triângulo é a metade da altura do primeiro, então seu perímetro também será.

Logo seus perímetros serão:  1 = 3  ;  2 = 1,5  ;   a3 =0,75  e assim sucessivamente

Temos então uma soma dos infinitos termos de uma PG de de razão = 1/2

S= a₁ / (1 – q) = 3 /(1 – 1/2) = 6

Prova de Matemática Comentada – UFRGS 2016 – Prova Resolvida

Questão 34. Resposta (E)

10^x = 20^y           = ?

log 10^x  = log 20

. log 10 = ∙ log(2 ∙ 10)

x .1 = y . (log2 + log10)

x/y = 0,3 + 1 = 1,3

Questão 35. Resposta (A)

Substituindo o valor de  x = 0 saberemos onde a função f(x) cortará os eixo das ordenadas.

y = f(x) = 1 – 5 . 0,7^x     

y = 1 – 5.0,7⁰ = 1 – 5 = -4

y = -4

para x = 0 teremos:  f(0) = 1 – 5 . 0,7⁰      ou  seja   y = 1 − 5.1 = -4 essas respostas eliminam (B) e (D).

A alternativa (E) não é uma curva exponencial por isso também não é valida.

Como é uma exponencial de base menor do que 1 o gráfico deverá ser decrescente porém temos um sinal de menos na frente da função. Isso gera uma imagem especular tornando a função crescente.

Questão 36. Resposta (B)

V = a . b . c

12 = ( + 4)( − 1)

12 = ³ + 3² − 4

³ − 3² − 4 − 12 = 0

Usando o método de tentativa para encontrar a primeira raiz encontramos o valor 2. Então dividimos o polinômio do terceiro grau por “x – 2” para encontrar as outras duas raízes. Como as outras raízes são negativas substituímos o número 2 para achar as medidas das dimensões da caixa.

x = 2 ;   x + 4 = 6     e    x – 1 = 1

Prova de Matemática Comentada – UFRGS 2016 – Prova Resolvida

Questão 37. Resposta (E)

A amplitude dos ângulos internos  “A” de um polígono é calculado por:

A= S_n/n    sendo S_n=soma dos ângulos internos de n lados  com S_n= (n-2) . 180

A= S_n/n

160 = (n-2) . 180 / n

160n =180n – 360

n = 18

Questão 38. Resposta (D)

Unindo-se os centros temos o valor de 2 Raios que é a diagonal do retângulo.

A altura do retângulo é o Raio = d_AB

Logo    10² = 5² +x² 

x = 5√3

A = B.H = 5 . 5√3 = 25√3

Questão 39. Resposta (A)

A = a . b . senx/2  = 1 . 1 . sen36⁰/ 2 = sen36⁰/ 2

Questão 40. Resposta (B)

V=  4πr³ / 3 . 0,5

2 L = 2000 ³

2000 ³ = 2πr³ /3   ssimplificando π/3 = 1 temos

= 10

Questão 41. Resposta (C)

O volume formado pela união dos pontos ACDH é  uma Pirâmide cuja base é o triângulo AHE e a altura é o lado DC

V = Ab . H / 3

V = (6.3/2 ).10 / 3

V = 30

Prova de Matemática Comentada – UFRGS 2016 – Prova Resolvida

Questão 42. Resposta (D)

Quando começamos a encher o recipiente a altura sobe rapidamente, pois o cone tem o seu vértice na parte de baixo. Conforme vamos preenchendo de água a altura tende a diminuir com o passar do tempo.

Dessa forma a função que indica  a altura em relação X tempo, será representado pela letra D

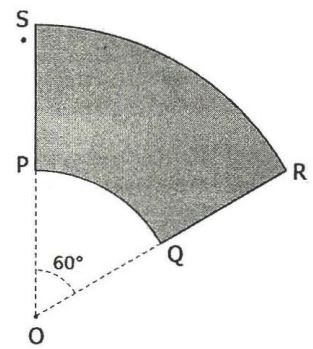
 Questão 43. Resposta (C)

O Comprimento SR = 2.π.R.60/360 = 2.π.6.60/360 = 2π

O Comprimento PQ = 2.π.r.60/360 = 2.π.3.60/360 = π

O comprimento SP e RQ tem valores iguais a 3

Perímetro da figura hachurada=  2.π + 3+ π +3

2P = 6 + 3 π

Questão 44. Resposta (B)

Vejam que esse tipo de questão sempre cai nas provas da UFRGS.

Cuidado pois não queremos saber quais são as Raízes e sim quantas vezes uma função encontra a outra no intervalo referido. Neste caso são 4 encontros ou seja temos 4 raízes.

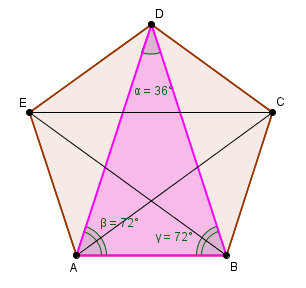
Questão 45. Resposta (C)

Considere um triângulo ABC qualquer de lados a, b e c:

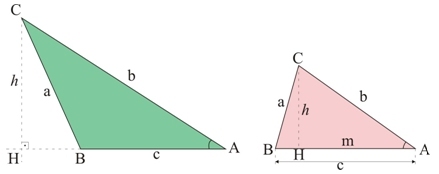
Para esses triângulos podemos escrever:

Nesse caso  o raio da circunferência é a distância entre dois vértices não consecutivos AC, BD, CE etc..

A distância AC é calculada pela lei dos cossenos onde o ângulo interno é 120⁰ e os lados do triângulo isósceles é 1

R² = 1² + 1² -2.1.1.cos120⁰

R² = 2 +2.√3

Área do Círculo = π.R = π.(2 +2.√3)

Questão 46. Resposta (E)

1) | x + 5| ≤ 2

x+ 5 = 2            x = -3

x + 5 = -2           x = – 7

2) | y – 4| ≤ 1

y – 4 = 1            y = 5

y – 4 = -1            y = 3

Pela análise dos pontos,  temos uma variação no eixo das abscissas o intervalo  (-3, -7)

Questão 48. Resposta (A)

1) 2L³ + 2²L = 180   indo temos        L³ + ²L = 90

2) 3L³ + ²L/ 3 = 110    ndo 3 temos    9L³ + ²L = 330

3) 2²L + 3 ²L/ 3 = 150

Aplicando um sistema com as 2 equações:

1) L³ + ²L = 90         L³ = 90 – ²L

9L³ + ²L = 330  substituindo 1 em 2

9(90 – ²L)  + ²L = 330

²L = 60

Substituindo em 1

L³ + ²L = 90

L³ + 60 = 90

L³ = 30        V_Cubo = 30

2²L + 3 ²L/ 3 = 150

3L³ + ²L/ 3 = 110

3.30 + ²L/ 3 =110  temos   ²L/ 3 = 20   ou seja V_cone = 20 cones

2²L + 3 ²L/ 3 = 150   temos    2,60 + 3 ²L/ 3 = 150

3 ²L/ 3 = 30      ²L/ 3 = 10   e V_pirâmde = 10

1 cubo + 1 cilindro + 2 cones + 2 pirâmides  pois:

30 + 60 + 2.20 + 2.10 = 150

Questão 49. Resposta (A)

Total de peças pretas  U = 16

Probabilidade= O que eu / tudo que tenho ℎ

P= n(A) /U = (8 /16). (7 /15) = 7 / 30

Questão 50. Resposta (D)

Como a probabilidade de acertar o alvo é 50%, então a área do  quadrado de lado x é 50

A= x²          50 = x²             x = √50 ≅ 7

Veja  a análise da prova no link abaixo

Clique Aqui – Comentário da prova