Terno Pitagórico – Macete Para Calcular Rapidamente Pitágoras [VÍDEO]

Muitos vestibulandos ainda não conhecem a expressão ” terno pitagórico primitivo ”, mas conhecer o que é e para que serve, pode ser de grande ajuda em uma prova cansativa e com muitos cálculos, como a prova do Enem, por exemplo.

Terno Pitagórico

Na realidade o terno pitagórico representa um trio de números naturais a, b e c tal que:                               

 a² = b² + c². 

Ou seja o terno pitagórico representa as medidas de dois catetos e da hipotenusa de um triângulo retângulo.

Como exemplo, podemos citar os famosos números 3, 4 e 5. Esse é o único trio de números que representam valores dessa relação, que são consecutivos.

Os números 3, 4 e 5 são considerados ternos pitagóricos, pois se enquadram na relação:

a² = b² + c²

5² = 4² + 3²

• Então o que é e quais são os mais famosos ternos pitagóricos primitivos que conhecemos?

Um terno pitagórico primitivo apresenta  três números primos entre si que se encaixam na relação:

a² = b² + c². 

São eles: (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29)… Verifique!

Exemplos de Ternos Pitagóricos

Você  pode observar que os ternos pitagóricos apresentam sempre um dos catetos impar e o outro par, sendo que a hipotenusa será sempre um número impar.

Os primeiro termos pitagóricos apresentam dois números consecutivos.

Se (a,b,c) é um terno pitagórico, então (ka,kb,kc) também é um terno pitagórico, para qualquer número natural k.

Matemática para Enem e vestibular

• E como esses números pitagóricos podem ajudar nos ajudar?

A técnica é simples e pode ser aplicada em todos os casos de ternos pitagóricos primitivos citados acima.

Técnica:

– Vamos usar o mais conhecido terno pitagórico que é o 3, 4 e 5

– Agora vamos multiplicar todos os números por 2 e o resultado fica:

3 x 2 = 6

4 x 2 = 8

5 x 2 = 10

Os novos números pitagóricos são:  6, 8 e 10

Observe que os novos números obtidos também são pitagóricos, pois:

10² = 6² + 8²

 – Agora vamos multiplicar todos os números por 3 e o resultado fica:

3 x 3 = 9

4 x 3 = 12

5 x 3 = 15

Os novos números pitagóricos são: 9, 12 e 15

Observe que esses números obtidos também se enquadram na relação:

15² = 12² + 9²

– Agora vamos multiplicar todos os números por 4 e o resultado fica:

3 x 4 = 12

4 x 4 = 16

5 x 4 = 20

Os novos números pitagóricos são: 12, 16, 20

20² = 16² + 12²
E assim por diante…

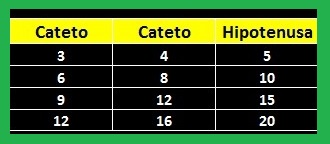
Terno Pitagórico primitivo

Veja abaixo o Vídeo explicativo, que mostra como usar com eficiência o Terno Pitagórico!

Vamos aplicar agora com outro trio pitagórico conhecido: (5, 12, 13)

Sabemos que 13² = 12² + 5²

– Agora vamos multiplicar todos os números por 2 e o resultado fica:

5 x 2 = 10

12 x 2 = 24

13 x 2 = 26

Os novos números pitagóricos são:  10, 24 e 26

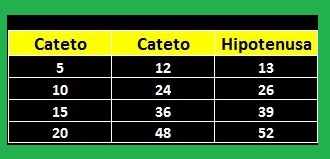
Terno pitagórico primitivo 2

Para concluir se você conhece o terno pitagórico primitivo, então facilmente poderá reconhecer os seus ternos derivados. Dessa forma não precisará calcular o terceiro lado usando o teorema de Pitágoras, onde o quadrado da hipotenusa é igual a soma dos quadrados dos catetos. Basta ver qual o número natural que multiplicou.

Vamos dar um exemplo

Conhecendo o terno primitivo, Tente encontrar o valor de x dos triângulos da figura, sem calcular por Pitágoras.

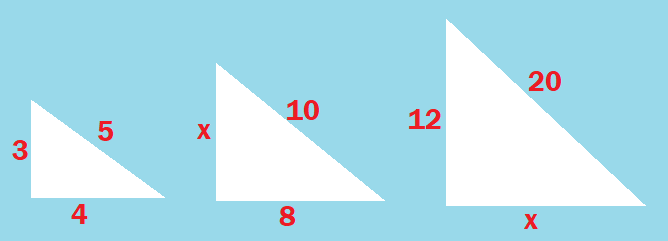
Terno Pitagórico – Macete

Veja aqui algumas aulas que poderão ser úteis na sua preparação:

1. Números Racionais Decimais e Periódicos
2. Tabuada Fácil, com as mãos
3. Sólidos de Platão
4. Problemas Matemáticos
5. Macete para MMC e MDC