Sólidos Geométricos de Platão – Poliedros [Vídeo]

O objetivo dessa aula é capacitar nosso leitor a calcular de forma fácil arestas, vértices e faces dos poliedros e mostrar a diferença entre os sólidos geométricos de Platão ou não!

A palavra poliedro é formada pela união do prefixo “poli = vários” + sufixo “edro =faces”.Esses sólidos apresentam  superfícies compostas apenas por polígonos planos.

Corpos redondos

Sólidos geométricos não poliédricos, são chamados de corpos redondos, quando apresentar pelo menos uma superfície arredondada.

Resumindo, assim como os corpos redondos, é uma forma espacial que possui pelo menos uma de suas faces não planas, os poliedros são sólidos geométricos que possui somente faces ou superfícies planas!

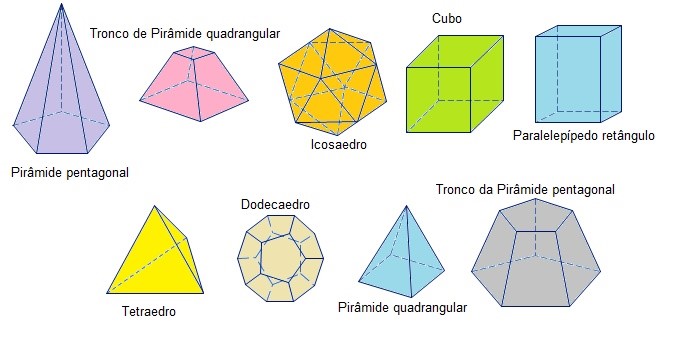
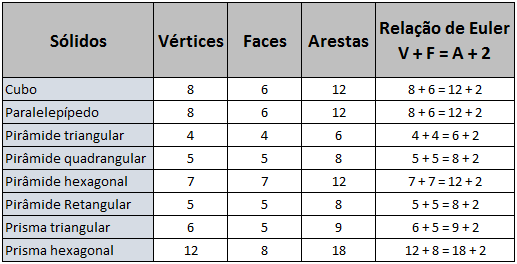
Veja abaixo uma lista de poliedros e suas nomenclaturas

Classificação dos poliedros

Podemos classificar os sólidos geométricos, chamados de Poliedros,  como  côncavos e convexos:

Convexo: um poliedro é convexo se qualquer segmento com extremidades dentro do poliedro estiver totalmente contido no poliedro.

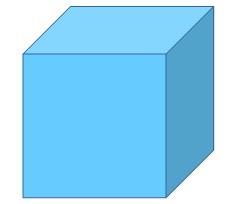
Cubo – Poliedro  Convexo

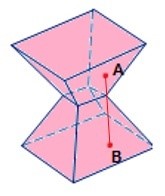
Côncavo: um poliedro é côncavo se algum segmento com extremidades dentro do poliedro possuir pontos fora do poliedro.

O poliedro acima é côncavo: o segmento de reta que parte de A e chega em B, tem pontos fora do poliedro.

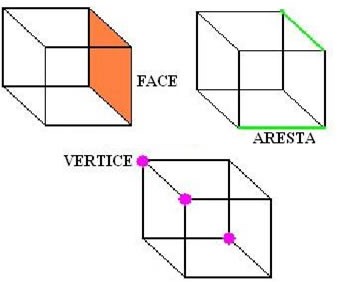
Sólidos geométricos multifacetados, chamados de poliedro, são compostos por 3 elementos importantes: arestas, vértices,  e faces.

Também podemos classificar um poliedro em regular e não regular

o mesmo será classificado como regular quando apresentar todas as suas faces congruentes, ou seja, todas as faces exatamente iguais.

Sólidos Geométricos de Platão

Esses poliedros regulares, também são chamados de Poliedros de Platão ou Sólidos Geométricos de Platão:

Dentre todos os sólidos geométricos existentes, há apenas 5  poliedros que se encaixam nesse conceito.

Para ser um Sólidos Geométricos de Platão é preciso:

1. Todas as faces devem possuir o mesmo número de arestas, além disso devem ser congruentes
2. De cada vértice deve partir o mesmo número de arestas
3. Precisa seguir com exatidão a relação de Euler.

Veja no vídeo abaixo tudo sobre os Sólidos Geométricos de Platão:

Poliedros regulares

Para um poliedro ser considerado regular é preciso que todos os seus lados e seus ângulos internos sejam exatamente iguais, ou seja congruentes.

Logo esse polígono ou poliedro poderá ser chamado de  regular ou de Platão se tiver as seguintes características:

1. Ser convexo.
2. Todas as suas faces são formadas por polígonos regulares e congruentes (iguais) entre si.
3. Todos os vértices formam ângulos congruentes (iguais).

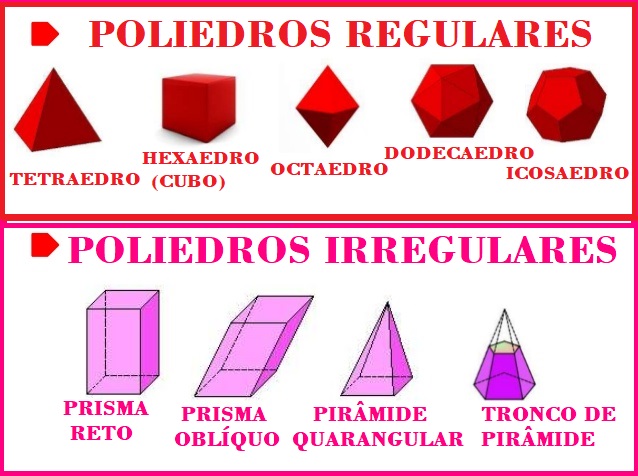
Como disse anteriormente, há apenas 5 Sólidos Geométricos de Platão. São eles: Tetraedro regular, hexaedro regular (cubo), octaedro regular, dodecaedro regular e icosaedro regular. Veja no desenho abaixo:

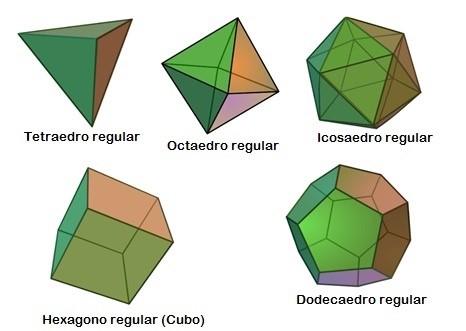
                                   Sólidos Geométricos de Platão

RELAÇÃO DE EULER

A relação de Euler é usada para relacionar o número de faces, vértices e arestas de poliedros convexos.

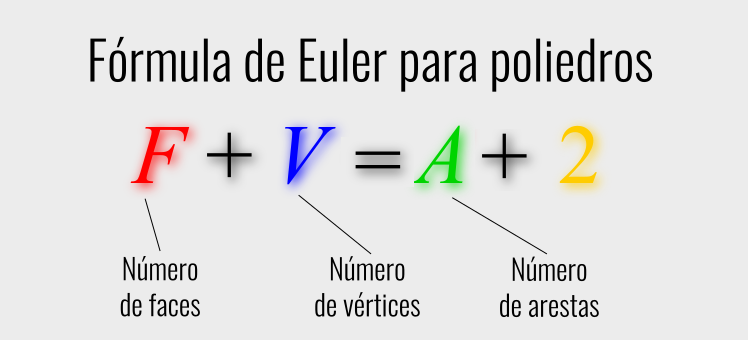
Relação de Euler – Fórmula de Euler

Outra relação importante nesse capítulo é a relação entre vértices e ângulos internos de um poliedro

A soma “S” dos ângulos das faces de um poliedro convexo que possui  “V” vértices é

S = 360º . ( V – 2)

Veja nesse vídeo alguns exercícios resolvidos sobre poliedros:

Veja aqui: 1) Macetes para resolver questões de MMC e MDC 

2) Macetes para calcular os ternos pitagóricos (Pitágoras)

Exercícios Resolvidos de Poliedros

1. Qual é o número de arestas de um poliedro convexo que tem 6 faces e 8 vértices. a) 8b) 10c) 12

   d) 14

   Resposta c

   Como a relação de Euler é válida para todos os poliedros convexos, temos: 

   V + F = A + 2

   A = 8 + 6 – 2

   A = 12 

   Portanto, esse poliedro convexo tem 12 arestas.

2. (UF – PI) Em um poliedro convexo, o número de arestas excede o número de faces em 18. O número de vértices desse poliedro é:a) 10
   b) 20
   c) 24
   d) 30
   e) 32Resposta  BTemos que:  A = F + 18.

   V + F = A + 2

   V + F = (F + 18) + 2 ⇒ cortando e anulando F temos:

   V = 2 + 18 ⇒ V = 20.

3. Determinar o número de arestas e o número de vértices de um poliedro convexo com 6 faces quadrangulares e 4 faces triangulares.

Solução:

 6 faces quadrangulares: 6 . 4 = 24

4 faces triangulares: 4 .3 = 12

Dica cada aresta sempre é contada duas vezes,logo o número total de arestas A é:

A = (24+12)/2 = 18

A = 36/2 = 18

Então já temos: F = 10  e A = 18. Agora é só achar V na relação de Euler

V + F = A + 2

V + 10 = 18 + 2 

V = 20 – 10 

V = 10

4) A soma dos ângulos das faces de um poliedro convexo é 2520º . Dê o número de faces desse poliedro , sabendo que ele possui 17 arestas .

Usando a fórmula

S = (V – 2).3600

25200 = (V – 2).3600

V – 2 = 7

V = 7 + 2 

V = 9

V + F = A + 2

9 + F = 17 + 2

F = 19 – 9 

F = 10